II. Practical Fundamentals of Astronomy
§ 4. Celestial Coordinates and Star Charts
Supplementary Materials for the Lesson
While there are approximately 6000 stars visible to the naked eye across the entire sky, we can only see half of them due to the Earth obstructing our view. As the Earth spins on its axis, our perspective of the sky changes. Certain stars are just appearing on the horizon (rising) in the eastern part of the sky, others are directly overhead at that moment, and some are already dipping below the horizon in the western part (setting). This creates the illusion that the entire sky is rotating. It is now common knowledge that this apparent rotation is actually caused by the Earth’s rotation.
By utilizing long exposure photography, it becomes possible to analyze the evolving pattern of the sky’s appearance caused by the Earth’s rotation.
Each individual star on the resulting image leaves behind a distinctive mark in the shape of a circular arc (see fig. 2.3).

The common point of origin for all these concentric arcs can be found in the celestial sphere near Polaris. This particular point, towards which the Earth’s axis of rotation is directed, is known as the North Pole of the World. The arc traced by Polaris has the smallest radius among all the arcs. However, regardless of their individual radii and curvatures, all these arcs collectively form a segment of the same circle. If it were possible to capture the paths of the stars in the sky throughout an entire day, the resulting photograph would display complete circles spanning 360 degrees. This is because a day represents a full rotation of the Earth around its axis. In the span of an hour, the Earth completes 1/24th of a circle, equivalent to 15 degrees. Consequently, the length of the arc traced by a star during this time period would be 15 degrees, and for half an hour, it would be 7.5 degrees.
To determine the location of the celestial bodies in the sky, we employ a coordinate system akin to the one employed in geography, namely the equatorial coordinate system.
As is widely known, the position of any given point on Earth can be denoted using geographical coordinates, specifically latitude and longitude. Geographical longitude (λ) is measured along the equator from the prime meridian (Greenwich), while geographical latitude (φ) is measured along the meridians from the equator to the poles of the Earth. For instance, Moscow is situated at the following coordinates: 37°30' East longitude and 55°45' North latitude.
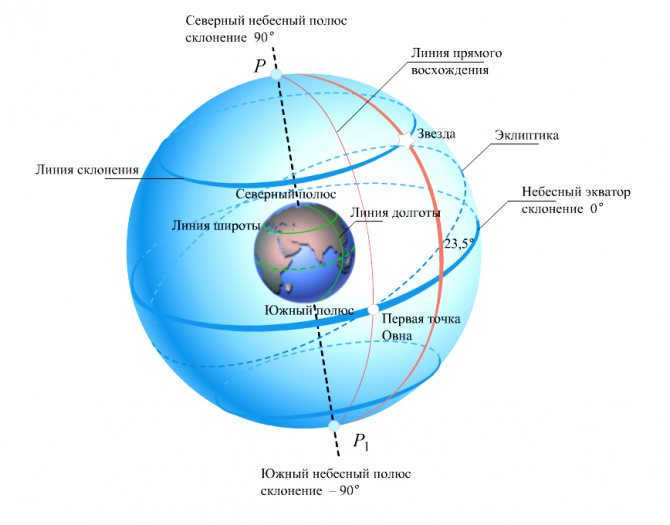
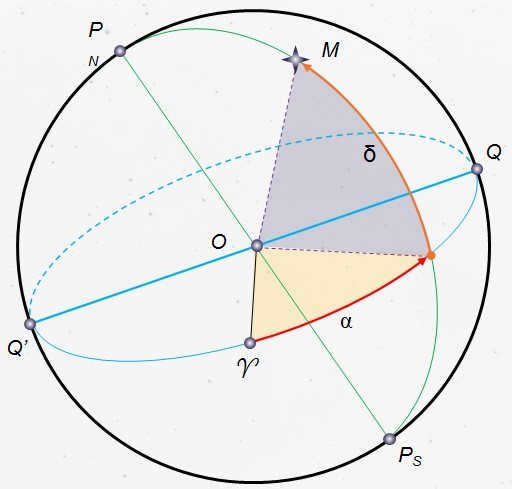
Let us familiarize ourselves with the equatorial coordinate system, which denotes the relative positions of the celestial bodies on the celestial sphere. We will depict a line that is parallel to the Earth’s rotational axis and passes through the center of the celestial sphere (Fig. 2.4) – referred to as the celestial axis.
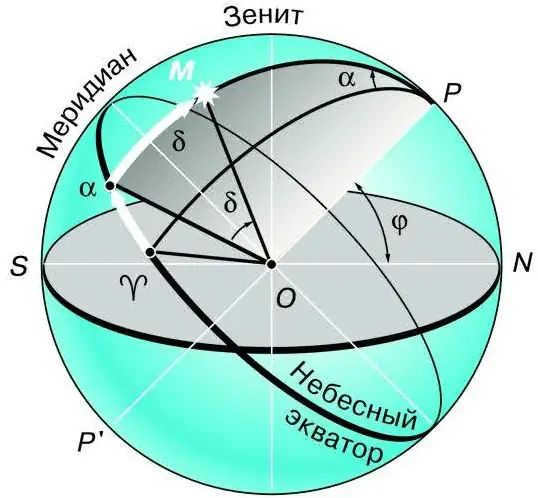
The second coordinate, known as the direct ascension (denoted by the letter a), is similar to geographic longitude and indicates the position of the luminary in the sky. It is measured along the celestial equator from the vernal equinox point ♈, which is where the Sun is on March 21st (the vernal equinox day) each year. The direct ascension is measured in the opposite direction to the apparent rotation of the celestial sphere. As a result, the luminaries rise and set in ascending order of their direct ascension. In astronomy, it is customary to express direct ascension in terms of hours rather than degrees. As you may recall, due to the Earth’s rotation, 24 hours correspond to 360°, and 1 hour corresponds to 15°. Therefore, a direct ascension of, for example, 12 hours is equal to 180°, and 7 hours and 40 minutes corresponds to 115°.
Using a star globe is not always convenient, which is why maps and atlases have become popular in astronomy, just like in geography. By projecting a hemisphere or another part of the Earth’s globe onto a plane, it is possible to obtain a map of the Earth’s surface. Similarly, by performing the same operation with a star globe, it is possible to create a map of the celestial sky.
Imagine placing the plane where we want to see the map so that it touches the surface of the globe at the point where the North Pole is located. Our goal is to project the stars and coordinate grid from the globe onto this plane. The result will be a map similar to Arctic or Antarctic geographical maps, with one of the Earth’s poles at the center. The North Pole of the world will be at the center of our star map, along with Polaris and other stars from the Little Bear and the Big Dipper constellations, as well as other constellations near the World Pole. The equatorial coordinate grid is represented on the map by rays that diverge from a central point and concentric circles. Each ray is labeled with numbers representing the hours of direct ascent (from 0 to 24 h). The ray that marks the starting point of direct ascent passes through the vernal equinox symbol, ♈. Declination is measured along these rays from the circle that represents the celestial equator, labeled 0°. The other circles are also marked to show the declination of objects located on each circle.
Stars on the map are depicted as circles with varying diameters, depending on their stellar magnitude. When stars form recognizable constellation shapes, they are connected by solid lines. The limits of constellations are indicated by dotted lines.
For more information on how to utilize the star chart for observation purposes, please refer to Appendix X.
Queries
1. What are the equatorial coordinates referred to as for a luminary?
2. Does the equatorial coordinates of a star undergo changes throughout the day?
3. Which characteristics of the diurnal motion of luminaries enable the use of an equatorial coordinates system?
4. Why is the position of the Earth not displayed on the star chart?
5. Why does the star chart exclusively depict stars and not the Sun, Moon, or planets?
6. What is the declination, either positive or negative, of stars that are closer to the center of the map than the celestial equator?
Exercise 3
1. Convert 90° and 103° to hourly measure.
2. Convert the direct ascension of 5 h 24 min and 18 h 36 min to angular measure.
3. The angular distance between Sirius (α of the Big Dog) and Polaris is 106°. Is Sirius’s declination positive or negative?
4. Locate some of the bright stars listed in Appendix V on a star map.
5. Determine the coordinates of several bright stars on the map. Compare the obtained data with the coordinates provided in their list.
Identify the major circles, lines, and points on a model of the celestial sphere: the horizon, celestial equator, celestial meridian, plumb line, world axis, zenith, south, west, north, and east.
In order to apply astronomical techniques, it is necessary to consider the celestial luminaries above the horizon. Therefore, it is essential for the navigator to be able to determine which luminaries will be non-sunrise, non-sunset, ascending, and setting during a given flight. To accomplish this, there are rules for determining the position of a luminary at the latitude of the observer’s location.
Figure 1.22 illustrates the celestial sphere from the perspective of an observer at a specific latitude. The straight line SJ represents the true horizon, while the straight lines and MJ depict the diurnal parallels of the celestial bodies. It is evident from the diagram that the luminaries can be categorized as non-setting, not ascending, ascending, or setting.
For this particular latitude, the luminaries whose diurnal parallels lie above the horizon do not set, whereas those with diurnal parallels below the horizon do not rise.
Luminaries positioned between the SC parallel and the North Pole of the world are considered non-setting. A luminary moving along the diurnal parallel of SC has a declination equal to the arc QC of the celestial meridian. The value of arc QC is obtained by adding the geographic latitude of the observer’s location to 90°.
Figure 1. 22. Conditions for the ascendancy and descendancy of celestial bodies
Therefore, in the Northern Hemisphere, the celestial bodies that do not descend will be those whose declination is equal to or greater than the complement of the observer’s latitude to 90°, i.e. . In the Southern Hemisphere, these celestial bodies will not ascend.
The non-superior luminaries in the Northern Hemisphere will refer to those luminaries whose diurnal parallels are between the MJ parallel and the South Pole. Clearly, the non-superior luminaries in the Northern Hemisphere will be those luminaries with a declination equal to or less than the negative difference, i.e. . For the Southern Hemisphere, these luminaries will be non-ascending. All other luminaries will be ascending and setting. In order for a luminary to rise and set, its declination must have an absolute value less than 90° minus the latitude of the observer’s location, i.e. .
Example 1. Star Aliot: determine the conditions of rising and setting for the given star at the specified latitude, taking into account the declination of the star and the latitude of the observer’s location.
Solution 1. Calculate the difference.
Example 2. Sirius, a star with a negative declination, has its latitude determined by the observer’s location. We need to determine when this star rises and sets at the given latitude.
Solution 1. By comparing the declination of Sirius with the obtained difference, we find that it has a negative declination.
2. After comparing the declination of Sirius with the obtained difference, we find that at the given latitude, Sirius does not have a declination.
Example 3. Arcturus, another star, also has its declination determined by the observer’s location. We need to determine when this star rises and sets at the specified latitude.
A group of stars within certain boundaries in the sky is known as a constellation. There are a total of 88 constellations, each recognizable by its unique arrangement of stars. Some constellations take their names from Greek mythology, such as Andromeda, Perseus, and Pegasus, while others are named after objects that resemble the shapes formed by the bright stars in the constellation, such as Arrow, Triangle, and Libra. There are also constellations named after animals, including Leo, Cancer, and Scorpio.
To locate constellations in the sky, one can mentally connect the brightest stars in a specific pattern. Within each constellation, the brightest stars are designated with Greek letters, starting with the brightest as alpha, followed by beta, gamma, and so on in alphabetical order. For example, the brightest star in the Little Bear constellation is Polaris.
Stars vary in brightness and color, with some appearing white, yellow, or reddish. The color of a star is an indicator of its temperature, with redder stars being cooler. Our Sun is classified as a yellow star.
Ancient Arabs assigned names to bright stars. Some notable examples include Vega in the Lyra constellation, Altair in the Eagle constellation (visible in summer and fall), and Sirius, which is the brightest star in the sky and visible in winter. Red stars include Betelgeuse in the Orion constellation, Aldebaran in Taurus (visible in winter), and Antares in the Scorpius constellation (visible in summer). Capella, a yellow star, can be found in the Ascendant constellation (visible in winter).
Stars are assigned fractional and negative stellar magnitudes based on precise measurements. For example, Aldebaran has a stellar magnitude of m=1.06, Vega has a magnitude of m=0.14, Sirius has a magnitude of m=-1.58, and the Sun has a magnitude of m=-26.80.
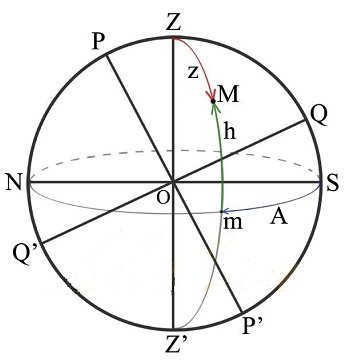
The daily motion of stars is studied using the celestial sphere, an imaginary sphere with an arbitrary radius centered around the observer’s point of observation. The axis of apparent rotation of the celestial sphere, which connects the two poles of the world (P and PV) and passes through the observer, is known as the world axis. The world axis for any observer will always be parallel to the Earth’s axis of rotation.
To create a star map that depicts constellations on a flat plane, one must know the coordinates of the stars. In the equatorial system, one coordinate is the declination, which represents the distance of a celestial body from the celestial equator. Declination ranges from +90° to -90°, with positive values north of the equator and negative values south. Declination is similar to geographic latitude. The second coordinate is known as right ascension and is comparable to geographic longitude.
Right ascension is measured as the angle between the planes of two great circles. One circle passes through the poles of the world and the celestial body, while the other passes through the poles of the world and the vernal equinox point located on the equator. The vernal equinox point is so named because on March 20-21, the Sun is in that position on the celestial sphere during the spring, when the day and night are of equal length.
Calculation of geographical latitude
The occurrence of the celestial bodies passing through the celestial meridian is referred to as culminations. The maximum height of a luminary is observed during the upper culmination, while the minimum height is observed during the lower culmination. The time gap between culminations is equivalent to half a day.
To determine the geographical latitude, one can measure the altitude of any luminary with a known declination during the upper culmination. It is important to note that if the luminary is located south of the equator at the time of culmination, its declination is negative.
The task. Sirius reached an altitude of 10 ° during its upper culmination. What is the latitude of the observation site?
Ecliptic. The apparent movement of the Sun and Moon
The altitude at which the Sun and Moon reach their highest point changes, indicating a change in their position relative to the stars (declination). We know that the Earth orbits the Sun and the Moon orbits the Earth.
When determining the Sun’s height at noon, it is observed that twice a year it aligns with the celestial equator during the spring and fall equinoxes (around March 21 and September 23). The celestial equator is divided in half by the horizon, so on these equinox days, the Sun’s path above and below the horizon is equal, resulting in equal day and night durations. On June 22, the Sun reaches its furthest point from the celestial equator towards the north pole of the world (at 23°27″). At noon in the northern hemisphere, the Sun is highest above the horizon (above the celestial equator). This day is known as the summer solstice, which has the longest duration of daylight.
The Sun’s path travels through 12 constellations known as the zodiac (from the Greek word “zoon” meaning animal), forming the zodiac belt. These constellations include Pisces, Aries, Taurus, Gemini, Cancer, Leo, Virgo, Libra, Scorpio, Sagittarius, Capricorn, and Aquarius. The Sun spends approximately one month in each zodiacal constellation. The vernal equinox point (where the ecliptic intersects the celestial equator) is located in the constellation of Pisces.
Task: Calculate the midday Sun height in Arkhangelsk and Ashgabat during the summer and winter solstices.
We can determine the approximate latitudes of Arkhangelsk (1) and Ashgabat (2) by referring to a geographical map. The declinations of the Sun during the summer and winter solstices are already known.
Using the formula:
Find:
1l = 48.5°, 1z = 1.5°, 2l = 75.5°, 2z = 28.5°.
Moon’s Movement. Solar and Lunar Eclipses

Lunar and solar eclipses are celestial events that occur when the moon or the sun temporarily blocks the light from the other celestial body. These phenomena are fascinating and have been studied by astronomers for centuries. During a lunar eclipse, the Earth’s shadow falls on the moon, causing it to darken and sometimes turn a reddish color. Solar eclipses occur when the moon passes between the Earth and the sun, blocking the sun’s light and casting a shadow on the Earth. Both types of eclipses are rare and occur only when the moon, Earth, and sun are aligned in a specific way. Scientists continue to study eclipses to learn more about our solar system and the universe as a whole.
Due to slight variations in the distances between the Earth, Moon, and Sun, the apparent size of the Moon can be slightly larger, slightly smaller, or equal to that of the Sun. In the first scenario, a total solar eclipse can last up to 7 minutes and 40 seconds. In the third scenario, the eclipse only lasts for a brief moment. In the second scenario, the Moon does not completely cover the Sun, resulting in an annular eclipse. During an annular eclipse, a bright ring of sunlight can be seen around the dark disk of the Moon.
Scientists have been able to accurately predict the timing and visibility of eclipses for hundreds of years based on precise knowledge of the Earth and Moon’s motion. Detailed maps have been created to show the path of the total eclipse, the areas where the eclipse will be visible in the same phase, and the specific moments of the beginning, middle, and end of the eclipse for different locations.
On Earth, there can be anywhere from two to five solar eclipses in a year, with some being partial. However, it is extremely rare to witness a total solar eclipse in the same location more than once every 200-300 years.
Solar eclipses occur when the Moon aligns between the Sun and the Earth during a new moon phase. During a total solar eclipse, the Moon completely obscures the Sun, causing sudden darkness and allowing the naked eye to see the faintly glowing corona of the Sun and the brightest stars.
The complete solar eclipse
Precise timing and geographical longitude
There are no specific guidelines for this subject. Please thoroughly read through the material. We wish you the best of luck.
If a star is non-setting, it means that when it reaches its lowest point (M΄) on the celestial sphere, it remains above the horizon. In the most extreme scenario, its height at the lowest point is zero. Let’s visualize this type of star on the celestial sphere. Its daily path is parallel to the equatorial plane and at its lowest point (M΄), it touches the horizon. From the diagram, it is evident that the minimum declination of a non-setting star is equal to
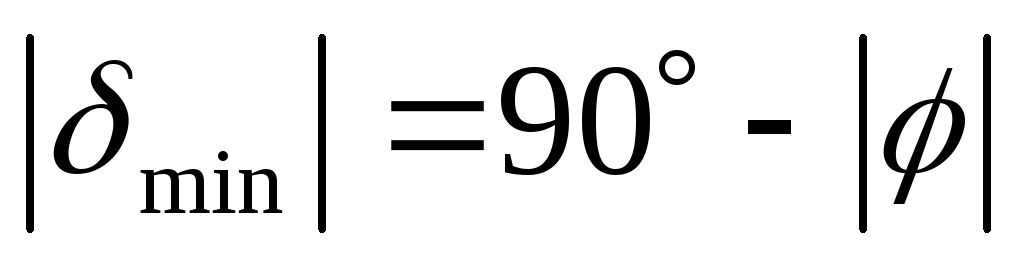
By substituting the latitude of Kaluga into the equation, we can determine the declination. As the star is situated in the northern hemisphere, the declination is positive. Hence, the conclusion is that in Kaluga, all stars with a declination greater than or equal to this value can be observed.
3. What is the declination of the star that reaches its highest point in Obninsk () at a certain altitude in the southern part of the sky? What would be the result if the star reaches the same altitude but north of the zenith?
Let’s visualize the celestial sphere and the star reaching its highest point to the south of the zenith. As the declination of the star is unknown, we can assume that it is negative, meaning the star is located south of the equatorial plane (refer to Fig. 3a) (Observant students can quickly deduce that the declination of the star is negative, as the angle between the equatorial plane and the horizon plane is equal to
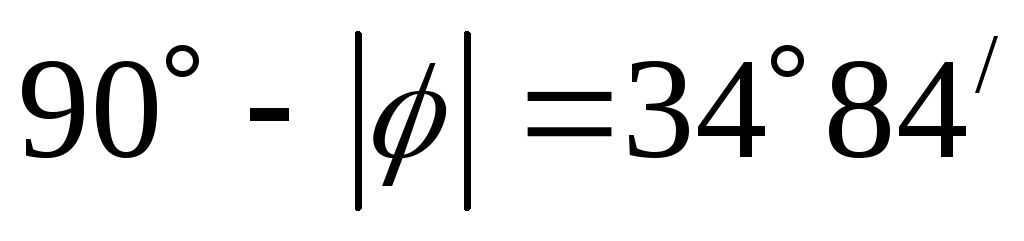
The star is positioned south of the equatorial plane, as the height at the upper culmination is greater than that of the star mentioned in the condition. The diagram clearly shows that the star is currently at its highest point.
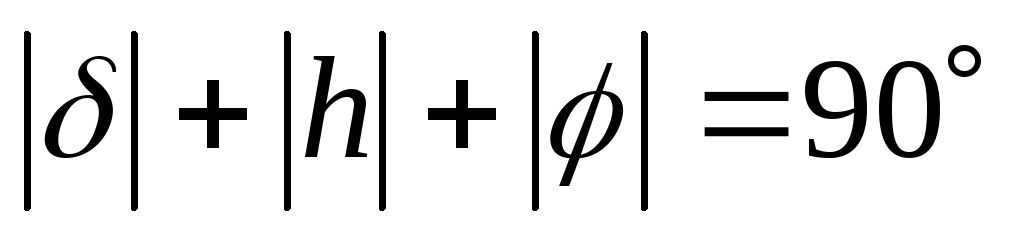
From where
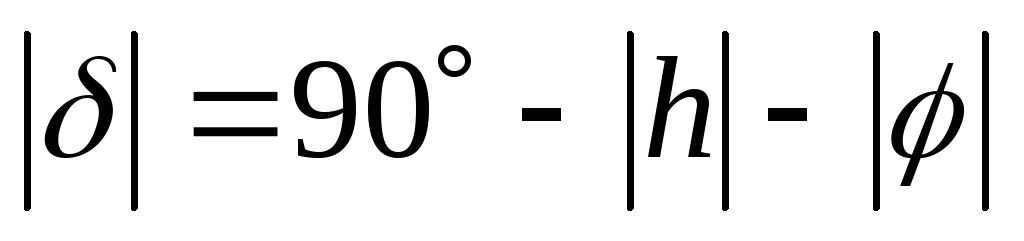
After replacing the numerical values, we get the following result. It appears that
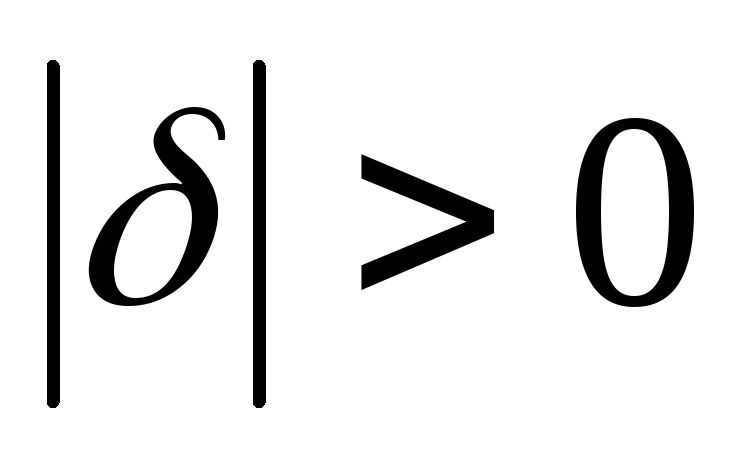
Therefore, the star is situated in the same position as we initially presumed, meaning that the star’s declination is indeed negative.
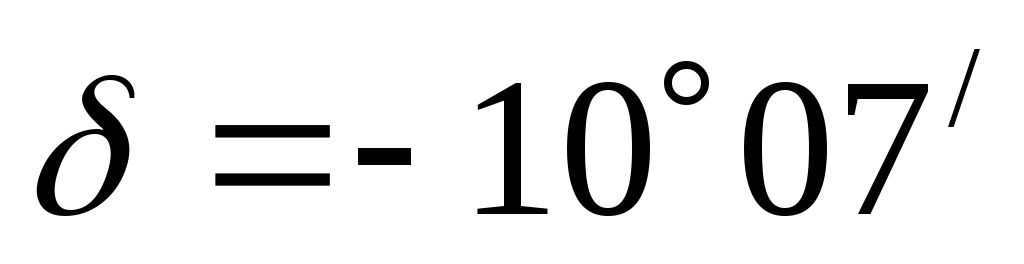
Suppose we assume that the star’s declination is positive, then we would find that .
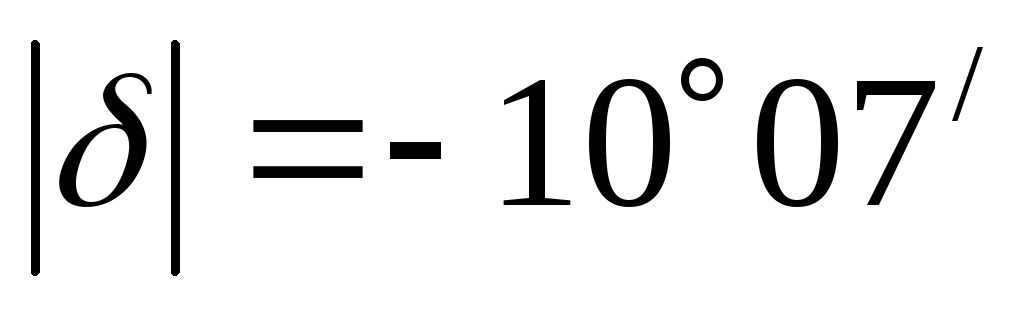
However, it is important to note that the modulus cannot be a negative number. Therefore, the initial assumption that the declination of the star is positive was incorrect. Nevertheless, the calculations were not in vain because the absolute value of the declination was still calculated correctly. In this case, however, the sign of the declination should be taken as the opposite.
Now let’s consider the second scenario (refer to Fig. 3b). If a star is visible in the northern hemisphere, specifically north of the zenith, its declination can only be positive. By analyzing the figure, we can deduce that this corresponds to the lower culmination of the star, and the following relationship holds true:
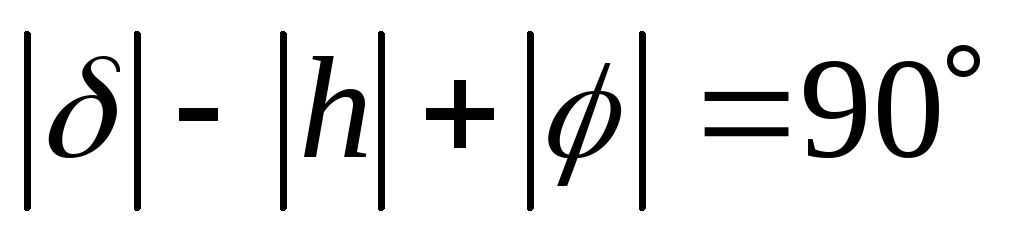
From where
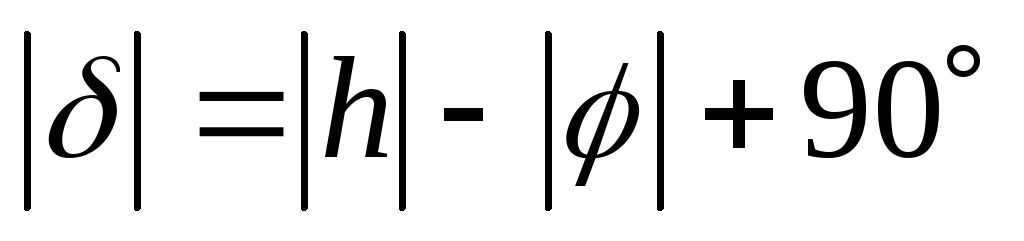
If we replace the numerical information, we get. Thus,

4. What is the highest altitude at which the star Mirfak (Perseus) can be seen in Spas-Demensk (N.S.) and Bucharest (N.S.), given its declination? On which side of the world is it currently visible?
Let’s visualize the celestial sphere in the diagram. Assuming that the star is observed south of the zenith during its upper culmination, we can clearly deduce from the diagram that
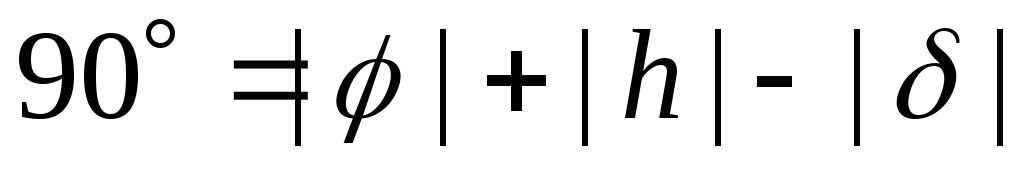
From where

.
Allow’s replace the numeric information. For Spas-Demensk we obtain,
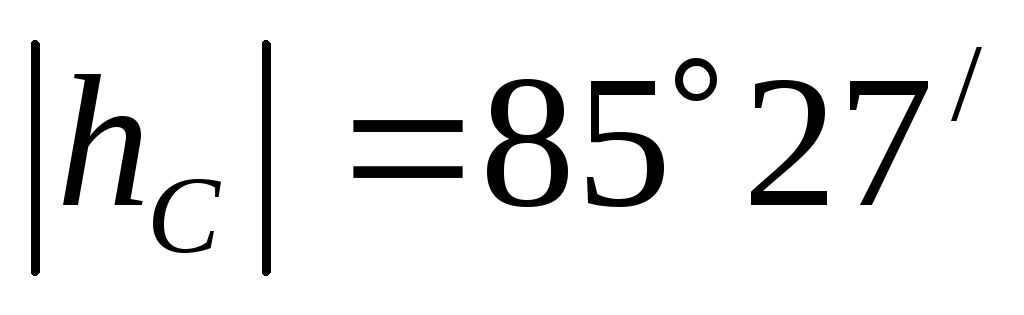
The height modulus was found to be a positive value and smaller than

The star’s height at the upper culmination in Spas-Demensk is equal to the maximum possible value of height, indicating that the position of the star was correctly chosen.
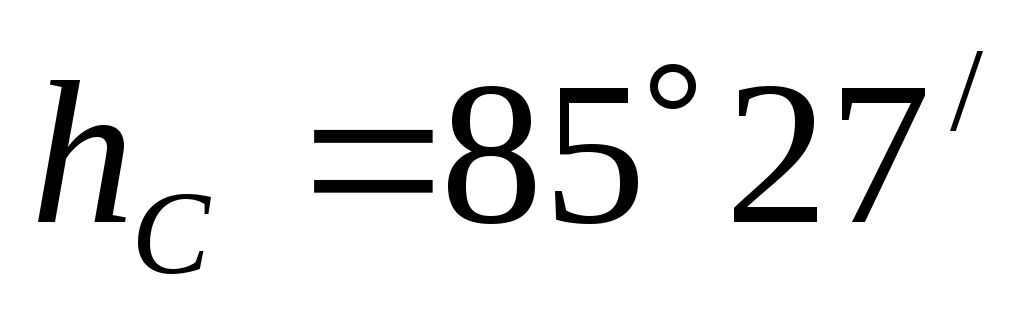
When it comes to Krasnodar, we end up with, that is to say.
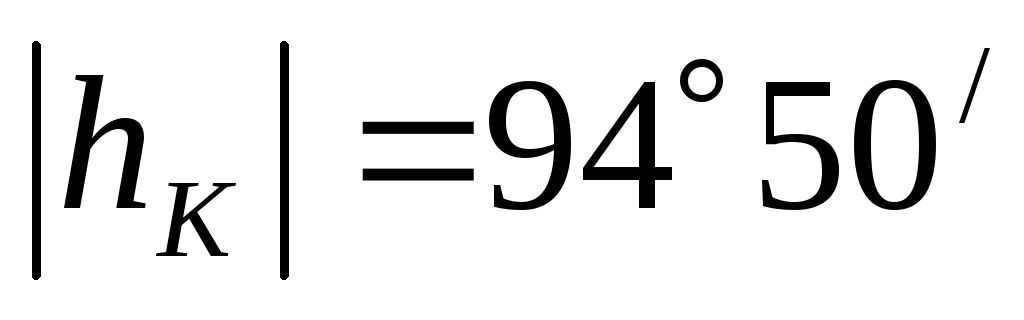
The measured value exceeds the maximum allowable height. This discrepancy can be resolved by considering that the altitude angle was measured from the southern point. Therefore, the star Mirfak reaches its highest point not to the south but to the north of the zenith in Krasnodar, and its altitude remains the same.
Thus, it is evident that the same star reaches a similar altitude at different latitudes but in opposite directions: in one case to the south and in the other case to the north.
Weak declension of adjectives
The weak declension of adjectives occurs when an adjective is preceded by certain words. These words include the definite articles der, die, das, die, as well as pronouns like dieser, jeder, jener, welcher, mancher, solcher, derselbe, derjenige. Additionally, pronouns such as alle, sämtliche, beide, keine, and possessive pronouns like meine, deine in the plural also trigger the weak declension of adjectives.
Declension of adjectives in the strong form
Adjectives are declined in the strong form when they are used in the following contexts:
1. When there is no accompanying word (pronoun, article).
2. After specific pronouns: viele, einige, mehrere, wenige, following the words verschiedene in plural form.
3. After specific numerals: etwas, genug, mehr, viel, wenig, nichts. Adjectives are capitalized after etwas and nichts:
Example: Ich habe etwas Neues erfahren. (I learned something new.)
4. After cardinal numerals (zwei, drei).
Example: Zwei neue Röcke habe ich mir in der vorigen Woche gekauft. (I bought two new skirts last week.)
| Kasus (Case) | Singular (Singular) | Singular (Singular | Plural (plural) | |
| maskulin (h. r.) | neutral (s. r.) | feminin (g. d.) | ||
| Nom. | great success | blue notebook | beautiful flower | big events |
| Gen. | great success’s | blue notebook’s | beautiful flower’s | big events’ |
| Dat. | to great success | to blue notebook | to beautiful flower | to big events |
| Akk. | great success | blue notebook | beautiful flower | big events |
The plate is made of pure gold. (A plate of pure gold .)
Black tea is consumed more frequently now. (Black tea is drunk more often now. )
They enjoy drinking fresh milk. (They like to drink fresh milk. )
Conjugation of adjectives with the indefinite article, negative pronoun kein and possessive pronouns in the singular number
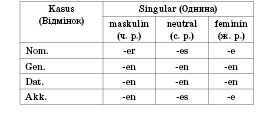
When combined with masculine, feminine, and neuter nouns, adjectives take on different endings depending on whether they are used with the indefinite article, the negative pronoun kein, or pronoun pronouns. Here are some examples:
- Ich habe mir ein neues Fahrrad gekauft. (I bought myself a new bicycle.)
- Ich brachte meinen kranken Hund in die Tierklinik. (I brought my sick dog to the veterinary clinic.)
- Du sollst kein trockenes Brot essen. (You must not eat dry bread.)
Adjectives have the ability to function as nouns. Substantive adjectives are modified by the articles der, die, ein, eine. When a substantive noun refers to a person, it can be either masculine or feminine. Substantive adjectives of the neuter gender are typically abstract in nature (das Äußere – appearance, das Neue – new).
| Case | Singular | Plural | ||
| masculine | neutral | feminine | ||
| Nominative | the old man | your exterior | the old woman | the sick |
| Genitive | of the old man | of your exterior | of the old woman | of the sick |
| Dative | to the old man | to your exterior | to the old woman | to the sick |
| Accusative | the old man | your exterior | the old woman | the sick |

If weather conditions are favorable, it is possible to observe the celestial sky in rural areas. It is composed of numerous luminous entities, commonly known as stars, whose radiance requires millions of years to reach our planet. Consequently, this image is a representation of the state of the universe during ancient times. Small groups of stars are referred to as constellations, while vast collections of stars are called galaxies.
Stars themselves are colossal celestial bodies with a significant gravitational pull, influencing the movement of planets, their satellites, asteroids, comets, and other celestial objects. A group of planets revolving around a star is known as a planetary system. On occasion, a planetary system may be composed of not one, but two stars at its core.
Stars are classified based on their temperature, which determines their color. The coolest stars are red, followed by orange, yellow, white, and blue. Stars can also be categorized by their size, with dwarfs and giants being the two main types. Generally, the brighter a star is, the smaller it tends to be. Eventually, a star may reach the end of its life and become a black hole, which has the ability to absorb all cosmic objects, including light.
Closest Stars
The closest star to Earth is the Sun, which is why our solar system is named after it. In ancient times, it was believed that the Earth was at the center of the universe and that the Sun revolved around it. However, in the 16th century, Nicolaus Copernicus proved that the Sun is actually at the center of our system. Compared to other stars, our Sun is quite ordinary in terms of its age, size, and brightness. It is classified as a yellow dwarf.
Scientists predict that in approximately 7 million years, the Sun will commence a gradual expansion, ultimately engulfing the neighboring planets, including our home planet Earth, transforming into a red giant. However, due to its insufficient mass, the Sun will not have the capability to evolve into a black hole and will eventually extinguish.
Proxima Centauri, the star closest to Earth, is classified as a red dwarf. The light emitted from this celestial body takes four years to traverse the vast expanse of space and reach our beloved planet. On the other hand, Sirius, one of the most luminous stars that grace the night sky, shines with a brilliance 25 times greater than that of the Sun, yet it is situated more than 500,000 times farther away.
Renowned constellations
One more shining star is Polaris, which belongs to the constellation of Ursa Minor. The names of most constellations have been passed down from ancient times: numerous star maps from that era depict symbolic depictions of constellations (such as Pisces represented as a fish or Lyra represented as a musical instrument). The actual shape of these constellations doesn’t always resemble their namesake, which is why the cluster of stars in the Big Dipper is often referred to as a “dipper”.
Stars Classification
The classification of stars is based on their size, color, and brightness. Stars are celestial bodies that can be seen as luminous dots in the night sky. Unlike planets and their satellites, stars emit their own light, and the color of this light is determined by the temperature of the star. The coolest stars are known as red stars (Figure 2).
Yellow stars, such as our Sun, are considered to be hot (Fig. 3). They have surface temperatures of over 10,000 degrees Celsius. On the other hand, white stars (Figure 4) have even higher temperatures.
Blue stars are the brightest of all and have a temperature of about 30 thousand degrees Celsius (Fig. 5).
There are stars that are a thousand times larger than the Sun in terms of size and mass, and there are also stars that are several times smaller than our planet.
The Sun is brighter than any other star in the sky because of its proximity to Earth.
It takes 8 minutes and 20 seconds for the Sun’s light to reach the surface of the Earth, while there are stars whose light takes thousands of years to reach us.
Constellations
In ancient Egypt, the observation of Sirius helped them predict the flooding of the Nile (Fig. 8).
In ancient Rome, Sirius was known as Canicula, meaning “the little dog” (Sirius is the brightest star in the constellation Canis Major, Fig. 9).
Figure 9. The constellation Canis Major ()
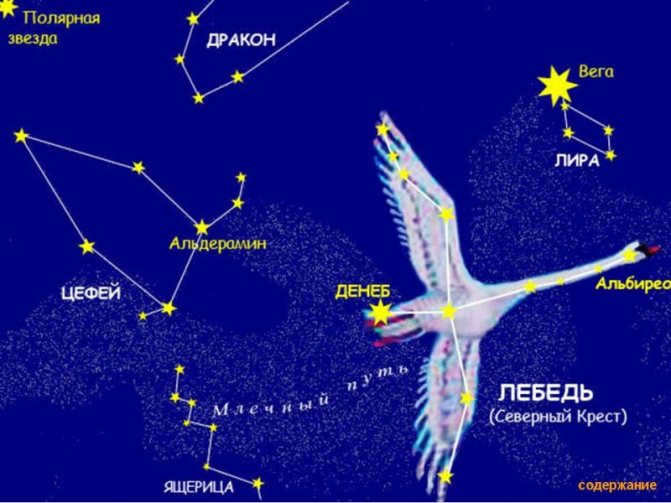
The time of year when people do not work or study is commonly referred to as a vacation. In ancient times, seafarers and travelers used the stars in the sky as a way to navigate and keep track of time. They noticed that the stars were grouped together, and so they divided the sky into 88 areas known as constellations. These constellations were named after animals, such as the Eagle, Dolphin, and Lizard. In the constellation of the Swan, the bright stars form a cross.
Figure 15. The Cross of the Swan constellation ().



- City of Bryansk
Bryansk serves as the administrative hub of the region with the same name, situated in the European part of Russia. It stands out as one of the oldest cities, established as a Slavic fortress in 985. Originally known as Debryansk, it has a rich history and cultural heritage. - Phraseologisms
In order for our speech to possess diversity, literacy, expressiveness, and alignment with the current norms of the Russian language, it is imperative to enrich our vocabulary and strive for its improvement. - Museum of Travels
When visiting a new city, we all have an innate desire to explore its captivating landmarks. One such intriguing tourist destination is the city of Almetyevsk, rightfully hailed as the capital of the oil region. It offers a plethora of sights and experiences for visitors to enjoy.
There is a different story surrounding the constellations that encircle the North Pole. In order to protect her newborn from the malevolent god Cronus, Zeus’ mother Rhea concealed him in a cave. There, he was nourished not only by the goat Amalthea, but also by two bears named Melissa and Helica. These bears were later immortalized in the heavens as constellations.
Fig. 16. The Big Dipper Constellation ()
Fig. 17. The Little Bear Constellation (
Fig. 18. The Volopassus Constellation ().
Polaris
In the Northern Hemisphere, there are two constellations that are easily visible: the Big Dipper and the Little Dipper (resembling two buckets). These constellations have become famous because of the star located on the handle of the Little Dipper. This star is called Polaris and it is known for pointing north. Because of this, it has been referred to as the “guiding star” by sailors and travelers (Figure 19).
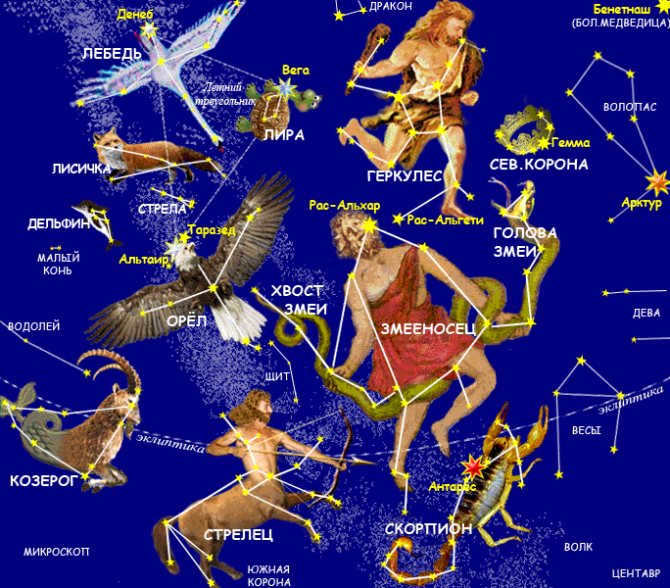
There are many constellations that have been named after mythical heroes, such as Andromeda, Hercules, Perseus, Cassiopeia, and Orion (Figures 20-24).
Fig. 20. Constellation Andromeda
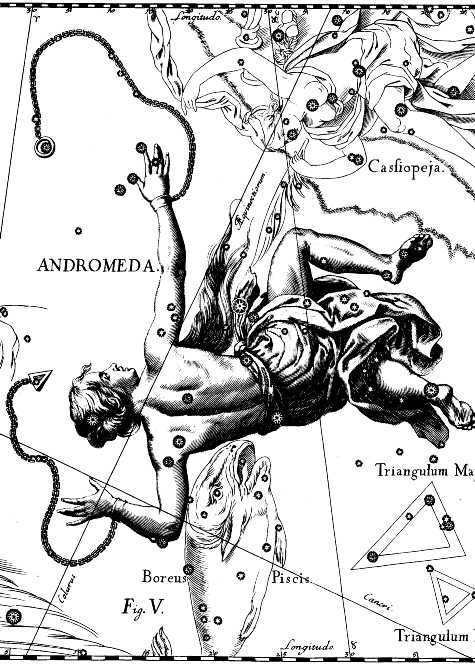
)
Figure 21. The arrangement of stars in the constellation of Hercules (
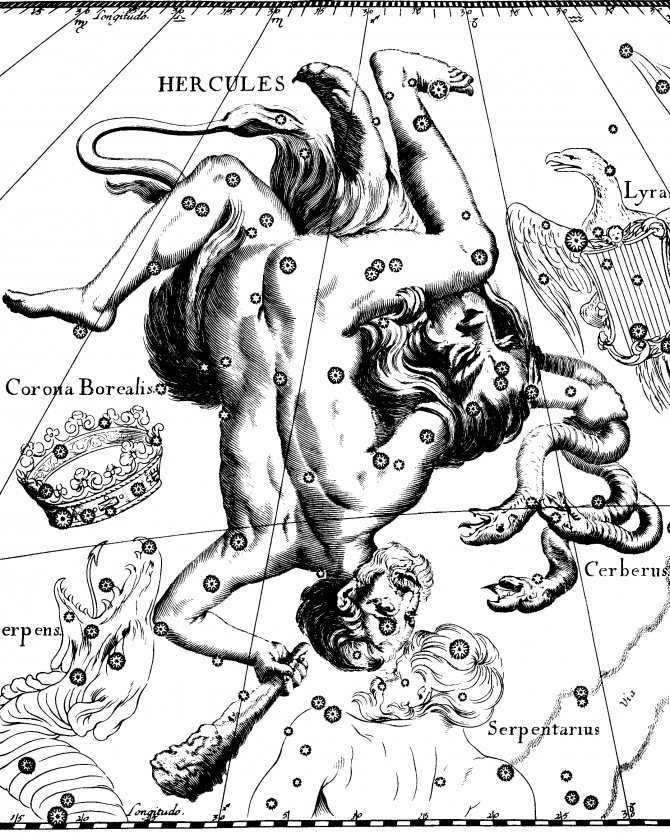
Figure 23. The arrangement of stars in the constellation of Cassiopeia.

(br)
INFOFIZ – my world …
Practical work No. 1
Topic: Exploring the night sky using a mobile star map
Objective: to become familiar with the mobile star map,
to learn how to determine the visibility conditions of constellations
Learn how to determine the coordinates of stars on the map
The appearance of the night sky changes due to the Earth’s daily rotation. The change in the view of the night sky depending on the time of year is caused by the Earth’s orbit around the Sun. This task is aimed at introducing the night sky, solving problems regarding the visibility conditions of constellations, and determining their coordinates.
The mobile star map is depicted in the image.
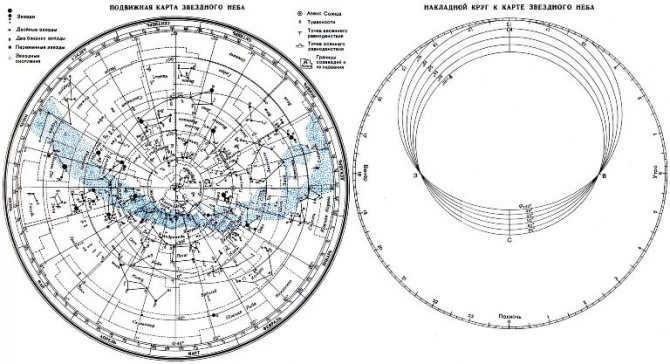
)
Prior to commencing work on the movable representation of the stars in the sky, it is necessary to cut the oval shape of the overlay circle along the line that corresponds to the geographical latitude of the observation location. The cut line of the overlay circle will serve as the horizon line. Affix the star map and the overlay circle onto the cardboard. Extend a thread from south to north of the overlay circle to indicate the direction of the celestial meridian.
- Stars are represented by black dots, with their sizes denoting their brightness;
- Nebulae are depicted with dashed lines;
- The center of the map shows the North Pole of the world;
- Lines originating from the North Pole of the world indicate the positions of declination circles. On the star map, the angular distance between the two nearest declination circles is 1 hour;
- The star chart includes celestial parallels plotted at 30-degree intervals, which can be used to calculate the declination of the luminaries δ;
- The points where the ecliptic intersects with the equator, with direct ascension of 0 and 12 h, are referred to as the points of the vernal g and W equinoxes;
- Along the edge of the star chart, months and numbers are marked, while the overlaid circle represents the hours;
- At the point of intersection of the filament representing the celestial meridian with the celestial parallel, whose declination is equal to the geographic latitude of the observation location, the zenith is located near the center of the cutout.
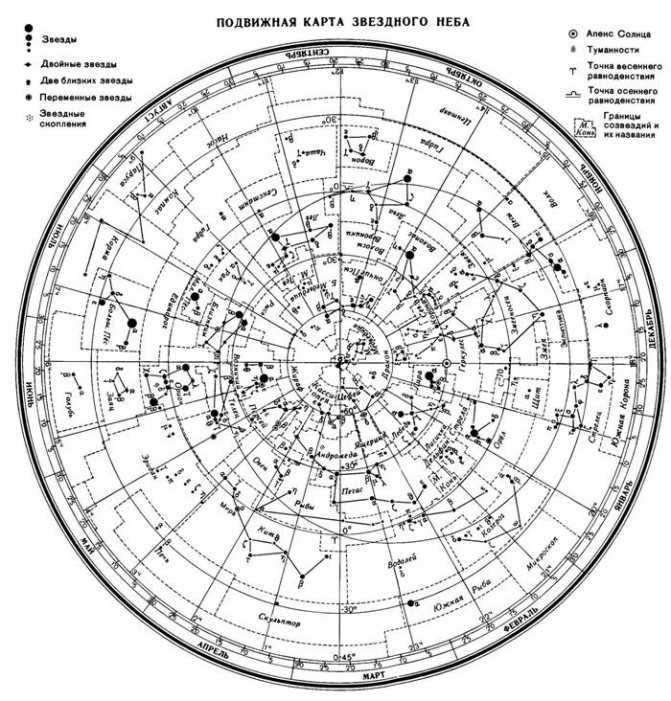
In order to ascertain the position of the celestial luminary, it is imperative to align the month, the specified number on the star chart, and the observation hour on the overlaid circle.
The celestial equator is a vast circle that encompasses the celestial sphere. It is positioned perpendicular to the Earth’s axis and aligns with the Earth’s equator. This celestial equator divides the celestial sphere into two distinct hemispheres: the northern hemisphere, which is located at the top of the world near the North Pole, and the southern hemisphere, which is situated near the South Pole. The constellations that intersect with the celestial equator are known as equatorial constellations. These constellations can be further classified as either southern or northern constellations.
In the Northern Hemisphere, notable constellations include the Big and Little Dippers, Cassiopeia, Cepheus, the Dragon, the Swan, the Lyre, the Magpie, and many others.
On the other hand, the Southern Hemisphere is home to constellations such as the Southern Cross, Centaurus, the Fly, the Sacrifice, and the Southern Triangle.
Nebula refers to a region in the interstellar medium that stands out due to its radiation or absorption of radiation compared to the general background of the sky. In the past, the term nebula was used to describe any extended object fixed in the sky. However, in the 1920s, it became clear that many nebulae are actually galaxies, such as the Andromeda Nebula. As a result, the term “nebula” started to be understood more specifically in the aforementioned sense. Nebulae are made up of dust, gas, and plasma.
Ecliptic pertains to the great circle of the celestial sphere along which the Sun’s visible annual motion takes place. The ecliptic plane represents the plane of the Earth’s revolution around the Sun, which is also known as Earth’s orbit.
The view of the starry sky and the daily movement of the stars vary depending on the observer’s location on Earth. The celestial sphere features circles as the daily paths of the stars, with their planes parallel to the celestial equator.
Now, let’s explore how the starry sky appears at the Earth’s poles. At the poles, the world axis aligns with a plumb line, and the horizon coincides with the celestial equator.
For an observer at the North Pole of the Earth, Polaris will appear directly overhead, and the stars will move in circles parallel to the mathematical horizon, which aligns with the celestial equator. Therefore, all stars with a positive declination will be visible above the horizon (conversely, at the South Pole, all stars with a negative declination will be visible), and their height will not change throughout the day.
Now, let’s consider the more familiar middle latitudes. Here, the Earth’s axis and the celestial equator are inclined relative to the horizon. As a result, the daily paths of the stars will also be inclined to the horizon. Therefore, observers at mid-latitudes will be able to observe stars rising and setting.
At sunrise, a luminary crosses the eastern part of the true horizon, while at sunset, it crosses the western part of the horizon.
In addition, some stars located in the northern circumpolar constellations never dip below the horizon, and are referred to as non-setting stars.
Similarly, stars near the South Pole for an observer at mid-latitudes are non-descending.
Now let’s consider the equator, where the geographical latitude is zero. Here, the world axis aligns with the noon line (in the plane of the horizon), and the celestial equator passes through the zenith.
The daily paths of every star, without exception, run perpendicular to the horizon. As a result, when positioned on the equator, the observer will have visibility of all the stars that rise and set throughout the day.
In general, for a celestial body to rise and set, its declination must be less than [insert value here].
If [insert value here], then in the Northern Hemisphere it will be non-ascending (and non-descending in the Southern Hemisphere).
Consequently, it is evident that celestial bodies with a declination of [insert value here] will not be visible in the Northern Hemisphere (or the Southern Hemisphere).
The equatorial coordinate system is a system of celestial coordinates that utilizes the celestial equator as its primary plane.
The equatorial celestial coordinates include:
2. The celestial body’s direct ascension (α) refers to the angular distance, measured along the celestial equator, between the vernal equinox and the point where the celestial equator intersects with the celestial body’s declination circle.
Procedure for conducting practical work:
Objectives of the practical work:
Objective 1. Determine the equatorial coordinates of Altair (α Eagle), Sirius (α Big Dog) and Vega (α Lyra).
Problem 2. Find the star using its coordinates on the starry sky map: δ = +35o; α = 1h 6m.
Objective 3. Determine which star δ of Sagittarius is for an observer located at latitude 55o 15ʹ. Determine whether the star is rising or not rising in two ways: using the overlapping circle of the moving starry sky map and using the formulas of the star visibility condition.
Also read: Teaching and methodological complex for the discipline 04 poetry of the silver age in school (ud-04 13-018)
Practical approach. We position the mobile circle on the star chart and determine whether the star is rising or setting by rotating it.
Theoretical approach.
We utilize formulas for determining the visibility of stars:
If , then the star is rising and setting.
If , then the star in the Northern Hemisphere is not ascending.
Task 4. Establish a mobile map of the starry sky for the designated day and time of observation, and identify the constellations situated in the southern part of the sky from the horizon to the celestial pole; in the east – from the horizon to the celestial pole.
Question 5. Identify the constellations that lie between the west and north points at 9 PM on October 10th. Verify the accuracy of this determination by visually observing the night sky.
Question 6. Locate constellations with nebulae marked on a star map and determine if they can be seen with the naked eye during the specified day and time of the lab work.
Question 7. Can you see the constellations Virgo, Cancer, and Libra at midnight on September 15th? Additionally, which constellation will be near the northern horizon at the same time?
Question 8. Determine which of the following constellations – Little Bear, the Little Knight, the Magpie, the Ascendant, or Orion – will remain visible at your latitude during unsunset hours.
Exercise 9. Locate and identify the approximate celestial coordinates (declination and right ascension) of the following constellations on the starry sky map: Ursa Major, Ursa Minor, Cassiopeia, Andromeda, Pegasus, Cygnus, Lyra, Hercules, Corona Borealis.
Issue 10. Determine which constellations will be visible near the horizon in the North, South, West, and East on the night of May 5th at midnight.
Review questions to reinforce the theoretical knowledge for the practical training:
2. What do constellations represent? (Constellations are divisions of the celestial sphere that serve as a guide for navigating the night sky. In ancient times, constellations were known as distinct patterns formed by bright stars.)
3. How many constellations exist today? (There are currently 88 recognized constellations. Each constellation varies in size and contains a different number of stars.)
4. Can you name some well-known constellations? (There are both prominent and lesser-known constellations. The notable ones include the Big Dipper, Hercules, Pegasus, Aquarius, Orion, and Andromeda. The lesser-known constellations include the Southern Cross, the Chameleon, the Flying Fish, the Small Dog, and the Bird of Paradise. Of course, these are just a few examples of the most famous constellations.)
5. What is a sky map? (A sky map is a representation of the starry sky or a portion of it on a flat surface. Astronomers have divided the sky map into two parts: southern and northern, similar to the Earth’s hemispheres).
6. What is the celestial equator? (The celestial equator is a large circle on the celestial sphere that is perpendicular to the axis of the Earth and aligns with the plane of the Earth’s equator.)
Upon completion of the practical work, the student is required to submit a report.
The report must include responses to all specified work instructions and answers to the control questions.
References:
1. Vorontsov-Vel’yaminov B. A., Straut E. K. “Astronomy. 11th grade”. Textbook with electronic appendix – M.: Drofa, 2017
2. In her book “Studying the starry sky with the help of a moving map,” R. A. Dondukova explores the use of a moving map to study the starry sky (Dondukova, 2000).
As scientists study space and the sky, they have discovered that everything is constantly in motion. The development of the coordinate system can be traced back to ancient times and is closely tied to the need for orientation on the terrain and understanding the structure of the celestial surface.

The expanse of the atmosphere beyond the billowy clouds
In order to ascertain the precise location and trajectory of celestial objects, humanity has devised an extensive array of techniques and methodologies. Furthermore, unique numerical and symbolic notations have been established. In actuality, there are several systems that determine the positional coordinates of celestial bodies. The primary distinctions between these systems lie in the selection of the primary plane and the point of reference. Given that the sky, as observed from Earth, appears as a spherical entity, the coordinates utilized in astronomy are inherently spherical. These coordinates represent various arcs of the sphere’s circles. It should be noted that these coordinates are typically measured in degrees, and occasionally in hours.
Horizontal coordinate system
The primary plane in the horizontal coordinate system is formed by the mathematical horizon, while the zenith and nadir represent the poles. This particular coordinate system is commonly employed for conducting observations from the Earth’s surface, whether it be with the unaided eye or through the utilization of a telescope. Its purpose is to facilitate the study of stars and the tracking of celestial objects as they traverse the sky, particularly within the confines of our solar system.
Horizontal coordinate system
Also, check out: Definition and types of ROO. Causes, striking factors, and medical consequences of an ROO accident. Zones affected by radiation contamination. The primary measures to protect the population in the event of a radiation accident.
Naturally, observation and measurement are ongoing as the movement of celestial bodies is constant.
Definitions in the coordinate system
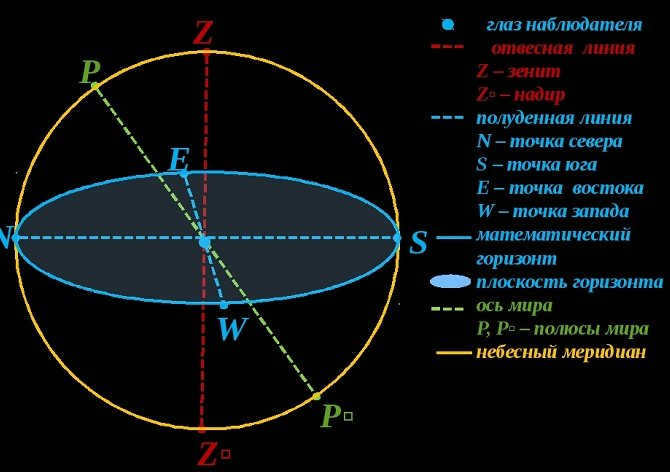
A vertical line is a straight line that passes through the center of the celestial sphere. It also aligns with the direction of gravity as perceived from the observation point. From the perspective of the observer, this line intersects the center of the planet and the observation site vertically.
Zenith and nadir are two opposite points. As we are aware, the vertical line intersects with the sky directly above the observer’s head, which is called the zenith. Conversely, the nadir represents the point diametrically opposite to the zenith.
The mathematical boundary refers to the celestial spherical surface’s great circle. It runs perpendicular to the vertical line and effectively divides the entire sky into two halves. These halves are known as the visible and invisible portions to the observer. The visible portion has its highest point at the zenith, while the invisible portion has its lowest point at the nadir.
Mathematical horizon, Zenith and nadir, Plumb Line
Simultaneously, the mathematical horizon does not align with the visible horizon. This is due to the uneven surface of the Earth and the varying highest point of observation. Additionally, the curvature of rays in the Earth’s atmosphere also plays a role.
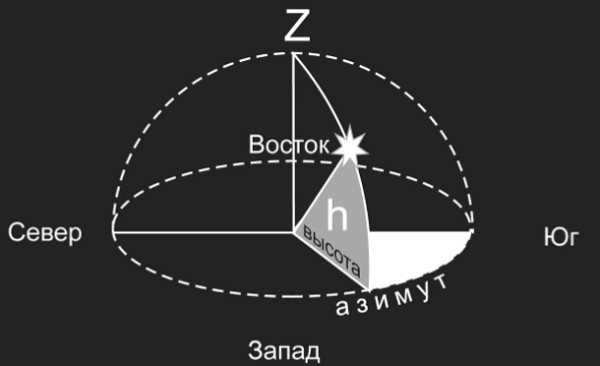
Azimuth
Methods for calculating geographic coordinates based on observations of celestial bodies.
The apparent motion of celestial bodies caused by their own movement in space, the rotation of the Earth, and its orbit around the Sun.
The Earth undergoes complex movements: it rotates on its axis (taking 24 hours), orbits around the Sun (taking 1 year), and also rotates within the Galaxy (taking 200 thousand years). This indicates that all observations made from the Earth exhibit distinct trajectories. The planets traverse the celestial sphere from east to west (known as direct motion) or from west to east (known as retrograde motion). The moments when the direction changes are referred to as risings. If you were to map this path, it would form a loop. The size of the loop decreases as the distance between the planet and Earth increases. The planets are categorized into lower and upper planets (lower planets, such as Mercury and Venus, are located inside the Earth’s orbit, while upper planets, including Mars, Jupiter, Saturn, Uranus, Neptune, and Pluto, are located outside). All of these planets orbit the Sun in a similar manner to the Earth, but due to the motion of the Earth, we can observe the looping motion of the planets. The relative positions of the planets with respect to the Sun and Earth are referred to as planetary configurations.
Planetary configurations refer to various spatial arrangements of the planets in relation to the Sun and Earth. These positions, which are observable from Earth and measured relative to the Sun, are given specific names. In the illustration below, denoted as V –
The inner planet, I, is the planet that is closer to the Sun. The Earth, E, is the inner planet. The outer planet, S, is the planet that is farther from the Sun. When the inner planet is in a straight line with the Sun, it is in a conjunction. The lower conjunction is when the inner planet is in a straight line with the Sun and the upper conjunction is when the outer planet is in a straight line with the Sun. The outer planet is in opposition when it is in the opposite direction to the Sun. The angle between the directions to the planet and to the Sun with its apex on Earth is called elongation. The maximum elongation for an inner planet occurs when the angle is 90 degrees. The maximum elongation for an outer planet also occurs when the angle is 90 degrees. The elongation can range from 0 degrees to 180 degrees. When the elongation is 90 degrees, the planet is said to be in the quadrature. The period during which a planet orbits the Sun is called the sideric orbital period, T. The period of time between two identical configurations is called the synodic period, S.
S – sideric period (relative to stars), T – synodic period (between phases), TÅ = 1 year.
Comets and meteoric bodies follow curved paths, including ellipses, parabolas, and hyperbolas.
The process of determining geographic coordinates through astronomical observations.
Geographic latitude and longitude are the two coordinates used to determine location. Astronomy provides practical methods for finding these coordinates. The distance between the celestial pole and the horizon corresponds to the geographic latitude of the observation site. An approximate geographic latitude can be determined by measuring the altitude of Polaris, which is approximately 10 degrees from the North Pole. The latitude of the observation site can also be determined by the height of a celestial body during its upper culmination (Culmination
– The formula for calculating the moment when the luminary passes through the meridian is: j = d ± (90 – h), depending on whether it reaches its highest point south or north of the zenith. The altitude of the luminary is represented by h, the declination by d, and the latitude by j.
The geographic longitude is the second coordinate, measured from the zero Greenwich meridian to the east. The Earth is divided into 24 time zones, with each zone representing a 1-hour time difference. The difference in local times is equal to the difference in longitudes:
Tl1 – Tl2 = l1 – l2. Therefore, by knowing the time difference between two points, with one point having a known longitude, we can determine the longitude of the other point.
The local time refers to the solar time at a specific location on Earth. Since the time varies at different points, individuals typically follow the time of the central meridian within their respective time zones. The international date line, which is located in the east (Bering Strait), marks the transition between different calendar dates.
To search for specific information, please utilize the site’s search function.
Introduction to the First Equatorial Coordinate System
The equatorial plane of the sky is considered as the flat surface in this particular system, with the reference point being Q. Moreover, the coordinates represent the declination and the hour angle. If you are wondering what declination is, you can find the explanation here. The hour angle refers to the arc that lies between the celestial meridian and the declination circle. Its measurement range is from 0° to 360°. It should be noted that the first equatorial coordinate system is used due to the continuous movement of our planet throughout the day. Therefore, the point of vernal equinox is established as the starting point, as it remains fixed relative to the stars.
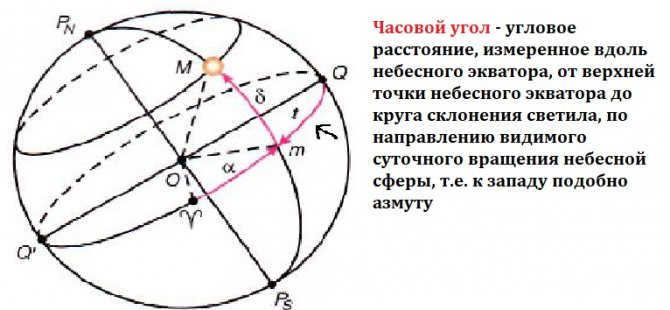
The hour angle
| Astronet Picture of the Day Astro-ph Reviews News Articles Books Sky Map Constellations Variable Stars A&ATr Glossary |
| planet Astronet Physics of Space Biographies Dictionary Keywords Astronomy in Russia Forums Seminars Supernovae |
Methods of teaching astronomy
§ 45. The altitude of celestial bodies and the latitude of the observing site.
There are two ways to conduct this exposition: 1) showcasing drawings of the firmament’s southern and northern halves for various locations on the Earth’s surface, and using this information to conclude how the height of the pole and equator change when moving across the Earth’s surface, ultimately proving that the height of the pole is equal to the latitude of the observation site; 2) initially proving that the height of the pole is equal to the latitude of the observation site, and using this deduction to determine the positioning of the celestial sphere in different locations on the Earth.
If we choose the first option, we would not be able to rely on the observations made by the students themselves. Since they are located in one specific place on Earth’s surface, they do not have a diverse range of observations regarding the changes in the arrangement of constellations in the sky. However, the preceding information provides enough evidence to make inferences and predictions about what can be observed at different latitudes. The ability to calculate and make inferences is valuable in a pedagogical context. Therefore, it is more preferable to choose the second option. By assuming that the axis of the Earth is parallel to the axis of the world, we can use traditional geometric methods to deduce the equality between the height of the pole and the latitude of a specific location. This conclusion should be further supported by visual representations, such as placing a model of a horizon with a celestial sphere in various locations on a globe, each with a corresponding inclination of the world’s axis. To demonstrate this concept, we can utilize a similar planar model developed by L.V. Kandaurov.
| Fig. 62. Drawing illustrating the calculation of the pole’s height above the horizon |
| Fig. 63. Diagram showing the areas where luminaries neither set nor surpass |
It is highly beneficial to demonstrate the simple derivation of the equator’s height above the horizon, as well as to verify that the declination of stars passing through the zenith of the observation location equals the latitude of that place (Fig. 62).
This conclusion can be easily understood and learned. It is important for students to understand that in astronomy, latitude is determined not only by the elevation of the celestial pole, but primarily by the zenith distance of Polaris (not the celestial pole) or any star with a known declination. The conclusion can also be presented as: h
= 900 – j + d and in the form j =
z
+ d. The second form is more straightforward, easier for students to remember, and aligns with the accepted convention in astrometry.
The conclusion can be derived using either the conventional method or by referring to Figure 62. Understanding this formula and its extension to negative declination and lower culmination allows for the concept of non-sunrise and non-sunset regions of the sky. The boundaries of these regions (depending on latitude) can be determined using these formulas (Fig. 63).
These conclusions are generally easy for students to grasp, but true comprehension requires constant illustrations on models of the celestial sphere, especially highlighting extreme cases at the equator and Earth’s poles.
The interest of students in different sky visibility conditions can be enhanced by providing examples from the accounts of travelers. For instance, in the book “Frigate Pallada” by I.A. Goncharov, there is a passage describing a sailor’s confusion about the movement of the Sun when the ship crosses the equator. The examples from the polar expeditions to North Pole stations are particularly compelling.
To illustrate the boundaries of the areas where the Sun does not rise and does not set on the celestial sphere, a star chart should be used. This chart should first depict the latitude of the city where the school is located, and then the two extreme latitudes of the USSR: 83° in the north and 36° in the south.
The representation of zenith distance using j and d is also significant because it allows for the measurement of d.
| Formula h | Formula z | Defined value | Measured value | Known quantity | Tool or method |
| 1) h = 900 – j + d | z = j – d | z | — | j and d | Calculation |
| 2)j = 900 – h + d | j = z + d | j | z | d | Universal tool |
| 3)d = h – 900 + j | d = j – z | d | z | j | Meridian circle |
The initial type of the relationship demonstrates the potential for performing a preliminary calculation of the zenith distance. The second and third perspectives illustrate the practical significance of this formula. The entry in the final column informs students about the specific angle measurement tools required to determine the sought values z, j, and d. As a result, the description of these tools is connected to certain theoretical considerations and practical requirements.
It is imperative to address all of these inquiries by examining the problems and selecting the most notable examples from contemporary practical applications.
The instructor needs to consider the question that arises with the most attentive students, which is the necessity of knowing d in order to deduce j (2nd type) and j in order to deduce d (3rd type). The student may suspect a circular reasoning here and question whether d can be practically ascertained.
The teacher should make it clear that astronomers have developed specific methods to avoid this harmful cycle. These methods involve using the upper and lower culminations of Polaris to determine the j and therefore the d of the observed star at the upper culmination, taking refraction into account.
Determining d from observations is a valuable concept that provides students with insight into how star charts are created and latitudes are determined in navigation and air navigation. It also highlights the interplay between theory and practice and the global significance of the Pulkovo Observatory.
Undoubtedly, the accuracy of latitude determination relies heavily on the precision of declination determination, which is acquired through observations made by meridian circles in observatories. These observations are carefully processed and included in fundamental catalogs. It is widely recognized that the Pulkovo Observatory has been consistently producing the most accurate determinations of star coordinates since its establishment. International catalogs place great importance on the data provided by Pulkovo, hence earning it the esteemed title of “the astronomical capital of the world.” Moreover, these stellar coordinates play a crucial role in enabling us to draw conclusions about the structure of our solar system and the known portion of the universe. While the teacher may not delve into these intricate details, it is imperative to provide students with a basic understanding of this significance. Once the principle of determining declination is explained, it would be beneficial to showcase a model of a meridian circle and discuss the Pulkovo Observatory, including its appearance following the restoration efforts undertaken after the destructive acts of the Nazis. In addition, it is worth mentioning the Soviet catalog of faint stars, which is compiled using photographic methods but relies on astrometric observations for its reference stars. For students who develop an interest in astronomy, an essay topic can be suggested: “Pulkovo Observatory.”
| Publications related to the following keywords: teaching methodology – teaching astronomy – teaching aids – demonstrations – starry sky – school atlas – star map – star charts – model – numerical modeling – observations – sundial – planetarium – lesson planning – visual aids Publications with the following words: teaching methodology – teaching astronomy – teaching aids – demonstrations – starry sky – school atlas – star chart – star map – star charts – model – numerical modeling – observations – sundial – planetarium – lesson planning – visual aids | |
| Also, take a look at: | |





