Newton’s law of universal gravitation provides a method for calculating one of the most important physical properties of a celestial object – its mass.
This can be done in several ways:
a) By measuring the gravitational force on the surface of the planet (gravimetric method),
b) Using Kepler’s third law,
c) Analyzing the observed perturbations caused by the planet on the motion of other celestial bodies.
1. The first method is commonly used for determining the mass of the Earth.
Based on the law of gravitation, the acceleration due to gravity at the Earth’s surface can be expressed as:
Where m is the mass of the Earth and R is its radius.
The values of G and R are measured at the Earth’s surface, with G being a constant.
By using the accepted values of g, R, and G, the mass of the Earth can be calculated:
To calculate the average density, we can utilize the given mass and volume data, resulting in a value of 5.5 g/cm3.
2. By applying Kepler’s third law, we can establish the relationship between a planet’s mass and the Sun’s mass, provided that the planet possesses a satellite and we know the distances and periods involved.
Here, M, m, and mc represent the masses of the Sun, the planet, and its satellite, while T and tc refer to the respective periods of orbit for the planet and satellite. Additionally, а and ace denote the distances from the Sun to the planet and from the planet to the satellite, respectively.
For all planets, the M/m ratio is significantly large, while the m/mc ratio is generally negligible, except in cases such as Earth and the Moon, Pluto and Charon.
The M/m ratio can be easily obtained using the provided equation.
To determine the mass of the Moon, we face the challenge of analyzing the perturbations it causes in the motion of the Earth. This task is quite difficult.
One approach to solving this problem is by examining the variations in the apparent positions of the Sun over time. These variations, known as the “lunar inequality,” occur on a monthly basis. They indicate that the center of the Earth follows a small elliptical path around the common center of mass of the “Earth-Moon” system. This center of mass is located inside the Earth, approximately 4650 km from its center.
Observations of the minor planet Eros between 1930 and 1931 also provided insights into the position of the Earth-Moon center of mass.
Based on fluctuations in the movements of man-made satellites orbiting the Earth, it was discovered that the mass ratio between the Moon and the Earth is 1/81.30.
This discovery was officially acknowledged as a constant by the International Astronomical Union in 1964.
Using Kepler’s equation, we can calculate that the mass of the Sun is 2.1033g, which is 333000 times greater than the mass of the Earth.
The masses of planets that do not have satellites are determined by the disturbances they cause in the motion of the Earth, Mars, asteroids, comets, and the perturbations they exert on each other.
The mass of the Sun can be determined by considering that the Earth’s gravitational pull towards the Sun acts as a centripetal force that keeps the Earth in its orbit (for simplicity, let’s assume the Earth’s orbit is a circle).
Here is the measurement of the Earth’s mass, the average distance between the Earth and the Sun. By denoting the duration of a year in seconds, we can determine the mass of the Sun:
The same equation can be used to calculate the mass of any planet that has a moon. In this scenario, we need the average distance between the moon and the planet, the time it takes for the moon to orbit the planet, and the mass of the planet. For instance, using the distance between the Moon and the Earth and the number of seconds in a month, we can find the mass of the Earth.
The mass of the Earth can be determined by equating the weight of any object to the gravitational force between that object and the Earth. This calculation is adjusted to account for the centripetal acceleration caused by the body’s participation in the Earth’s daily rotation. However, this correction is not necessary if we use the gravitational acceleration observed at the Earth’s poles. Denoting the average radius of the Earth as R and the mass of the Earth as M, we can express this as:
If we denote the average density of the Earth as ρ, then it is clear that the average density of the globe is equal to the average density of the Earth.
The average density of the mineral rocks in the upper layers of the Earth is approximately equal to. This implies that the density of the Earth’s core must be significantly higher than the average density of the entire planet.
Lejeandre and several other scientists have conducted extensive research on the density of the Earth at different depths. According to the findings of Gutenberg and Gaalk (1924), the density of the Earth varies at different depths:
The pressure inside the Earth’s core is believed to be extremely high, especially at great depths. Many geophysicists hypothesize that the pressure at these depths could reach several atmospheres per square centimeter. In the core of the Earth, which is estimated to be around 3000 kilometers deep or even deeper, the pressure is thought to reach 1-2 million atmospheres.
Regarding the temperature beneath the Earth’s surface, it is a known fact that it is significantly higher, similar to the temperature of lava. In mines and boreholes, the temperature increases by approximately one degree for every unit of depth. Let’s assume that at a certain depth, around 1500-2000°, the temperature stabilizes and remains constant thereafter.
Take a look at Figure 50, which illustrates the relative sizes of the sun and planets.
The complete theory of planetary motion, as described in celestial mechanics, enables us to determine the mass of a planet based on its gravitational influence on another planet. In the early 19th century, scientists were aware of the existence of Mercury, Venus, Earth, Mars, Jupiter, Saturn, and Uranus. However, they noticed that Uranus exhibited some irregularities in its motion, suggesting the presence of an unseen planet affecting its orbit. In 1845, French scientist Leverrier and Englishman Adame independently studied the motion of Uranus and calculated the mass and position of a yet-to-be-discovered planet. Subsequently, a planet was observed in the exact location predicted by their calculations, and it was named Neptune.
In 1914, Lovell, an astronomer, made a similar prediction about the existence of another planet, which was believed to be located even further away from the Sun than Neptune. However, it wasn’t until 1930 that this planet was finally discovered and given the name Pluto.
Provided in the table below is some basic information about the nine major planets that make up our solar system. Additionally, Figure 50 visually demonstrates the relative sizes of both the Sun and these planets.
Aside from the aforementioned large planets, there are also approximately 1300 much smaller planets known as asteroids (or planetoids). These asteroids primarily orbit between the paths of Mars and Jupiter.
The Earth is a distinctive planet within our solar system. It may not be the smallest, but it certainly isn’t the largest either, ranking fifth in terms of size. Among the planets in the Earth’s group, it holds the record for being the largest when it comes to mass, diameter, and density. Being situated in outer space, it becomes quite challenging to determine the Earth’s weight. Unlike objects that can be placed on a scale and directly weighed, the Earth’s weight is calculated by adding up the masses of all the substances it comprises. This calculation yields an approximate weight of 5.9 sextillion tons. To truly comprehend the enormity of this figure, one can simply write it down mathematically as 5,900,000,000,000,000,000,000. The sheer magnitude of zeros in this number is enough to make one’s eyes water.
The Quest to Determine the Earth’s Size Throughout History
Throughout the ages, scientists from various cultures and time periods have undertaken the challenge of uncovering the true weight of our planet. In ancient times, it was widely believed that the Earth was a flat surface, supported by whales and turtles, or sometimes elephants, at its edges.
As the Middle Ages dawned, new ideas emerged regarding the shape and weight of the Earth. One notable figure, J. G. W. H. W. Baker, was the first to propose a spherical form for our planet. Tragically, Bruno paid the ultimate price for his revolutionary beliefs, as he was executed by the Inquisition. Another significant contribution to our understanding of the Earth’s size came from the intrepid explorer Magellan, who put forth the notion that our planet was indeed round.
Initial findings
The planet Earth is a physical entity possessing distinct characteristics, one of which is its weight. This revelation served as a catalyst for numerous investigations to commence. According to principles in physics, weight is the result of the gravitational force exerted by an object on its support. Considering that the Earth lacks any specific support, it can be inferred that it does not possess weight, but it does possess an immense mass.
The Mass of the Earth
Eratosthenes, an ancient Greek scientist, was the first person to attempt to determine the size of the planet. He measured shadows in different cities of Greece and compared the data in order to calculate the volume of the Earth. Following him, the Italian scientist G. Galileo made his own calculations and discovered the law of free gravity. Continuing this line of research, I. Newton took on the task of determining the mass of the Earth and, through his measurements, discovered the law of gravity.

In a groundbreaking discovery, Scottish scientist N. Makelin successfully determined the precise weight of the Earth. Based on his calculations, the planet weighs approximately 5.9 sextillion tons. However, it is important to note that this figure is subject to change. Variations in weight can be attributed to the accumulation of cosmic dust on the planet’s surface. Approximately thirty tons of dust settle on the Earth each year, contributing to its increasing weight.
Mass of the Earth
To determine the precise weight of planet Earth, it is essential to have knowledge of the composition and weight of the various substances that constitute the planet.
- Mantle. The mass of this layer is approximately 4.05 X 10 24 kg.
- Core. This layer is lighter than the mantle, weighing only 1.94 X 10 24 kg.
- Crust of the Earth. This part is very thin and has a weight of only 0.027 X 10 24 kg.
- The hydrosphere and atmosphere. These layers have weights of 0.0015 X 10 24 and 0.0000051 X 10 24 kg, respectively.
By adding up all of these measurements, we can calculate the total weight of the Earth. However, different sources may provide slightly different values for the mass of the planet. So, how much does planet Earth weigh in tons, and what are the weights of other planets? The weight of the Earth is approximately 5.972 X 10 21 tons. The Earth has a radius of 6,370 kilometers.

By utilizing the concept of gravity, it is possible to easily ascertain the mass of our planet Earth. In order to accomplish this, a thread is utilized upon which a small weight is suspended. The precise location of the weight is determined. A ton of lead is then placed adjacent to the weight. Due to the gravitational attraction between the two bodies, the weight deflects to the side by a minuscule distance. Even a deviation as small as 0.00003 mm allows for the computation of the Earth’s mass. This is achieved by measuring the attraction force between the weight and the Earth as well as the attraction force between the small weight and the larger one. The acquired data enables the calculation of the Earth’s mass.
The weight of the Earth and other planets
The Earth is the biggest planet in our solar system. In comparison, Mars has a weight that is approximately 0.1 times that of the Earth, while Venus has a weight that is about 0.8 times that of the Earth. The gas giants, on the other hand, are much larger than Earth. When comparing Jupiter to our planet, it is 317 times bigger and Saturn is 95 times heavier. Uranus, on the other hand, is 14 times heavier. There are even planets that weigh 500 times or more than the Earth. These massive gas bodies can be found outside of our solar system.
The law of universal gravitation, expressed by f-law:
(1)
states that the force of mutual attraction between two masses, denoted as F, is proportional to the product of their masses and inversely proportional to the square of the distance r between their centers. In the field of astronomy, the size and shape of celestial bodies are often disregarded, treating them as point masses where their entire mass is concentrated.
The constant of gravitation, denoted as G, is the coefficient of proportionality. It can be determined through a physical experiment involving torsion weights, which allows for the measurement of the gravitational force between bodies of known mass.
When bodies fall freely, the force F that acts on them is equal to the product of their mass and the acceleration of free fall, g. The value of g can be determined by measuring the period T of oscillation of a vertical pendulum, where l is the length of the pendulum. At a latitude of 45 degrees and sea level, g is equal to 9.806 m/s^2.
The formula (1) can be used to determine the mass of the Earth by substituting the expression for the Earth’s gravitational forces. This leads to the dependence , where represents the mass of the Earth and is the radius of the globe. The determination of the Earth’s mass is crucial for calculating the masses of other celestial bodies such as the Sun, Moon, planets, and stars. The masses of these bodies can be determined using Kepler’s 3rd law or the rule that states the distances of any masses from the common center of masses are inversely proportional to their masses. By applying this rule, we can determine the mass of the Moon. Observations of the exact coordinates of the planets and the Sun reveal that the Earth and the Moon orbit around the barycenter, which is the center of mass of the Earth-Moon system, with a period of one month. The distance of the Earth’s center from the barycenter is 0.730 (located inside the globe), while the distance of the Moon’s center from the Earth’s center is 60.08 . Therefore, the ratio of the distances of the centers of the Moon and the Earth from the barycenter is 1/81.3. Since this ratio is the inverse of the ratio of the masses of the Earth and the Moon, the mass of the Moon is 1/81.3.
г.
The Sun’s mass can be calculated by using Kepler’s 3rd law to examine the movement of the Earth (along with the Moon) around the Sun and the Moon’s movement around the Earth:
, (2)
where a – represents the major semi-major axes of the orbits, T – represents the periods (stellar or sideric) of the orbit. By neglecting compared to , we find the ratio , which equals 329390. Therefore, g, or approximately .
The masses of planets with satellites are determined in a similar manner. The masses of planets without satellites are determined by analyzing the perturbations they cause in the movements of their neighboring planets. The theory of perturbed planetary motion allowed for the suspicion of the then-unknown planets Neptune and Pluto, the determination of their masses, and the prediction of their positions in the sky.
The determination of the mass of a star (excluding the Sun) can be done with a reasonably high level of accuracy only when it is part of a visual double star system, where the distance between the stars is known. Kepler’s third law can be applied in this case to calculate the sum of the component masses (in units ):
,
where а "" represents the major semi-axis (in seconds of arc) of the true orbit of the companion star around the main star (usually the brighter one), which is assumed to be stationary in this scenario, and Р represents the orbital period in years, – of the system (in seconds of arc). The value gives the major semi-axis of the orbit in a. e. If the angular distances of the components from the common center of mass can be measured, their ratio can be used to determine the inverse ratio of their masses: . By knowing the sum of the masses and their ratio, the individual mass of each star can be obtained. If the double star components have similar luminosity and spectra, then the half-sum of the masses can be used to estimate the mass of each component without needing to determine their ratio separately.
When it comes to other categories of double stars like eclipsing-doubles and spectral-doubles, there are several options available to approximate the masses of the stars or to determine their minimum values (i.e., the values that their masses cannot be less than).
By aggregating data on the masses of approximately one hundred double stars of various types, we have been able to uncover a significant statistical correlation between their masses and luminosities (refer to ). This correlation allows us to estimate the masses of individual stars based on their (or rather, their abs. ). The absolute magnitudes of stars, denoted as M, can be determined using the following formula: M = m + 5 + 5 lg – A(r) , (3) where m represents the apparent magnitude of the star in the specified optical range (within a specific photometric system, such as U, V, B, etc.). U, V, or V ; see (e.g., U, B, or V). ), reflects the parallax, and A(r) denotes the magnitude of light in the same optical range along a given direction up to a certain distance .
If the parallax of a star is not measured, an estimation of the star’s absolute magnitude can still be derived from its spectrum. To achieve this, the spectrogram must not only identify the stars, but also allow for the estimation of the relative intensities of certain pairs of spectral lines that are sensitive to the “absolute magnitude effect”. In simpler terms, the first step is to determine the star’s luminosity class – its classification within one of the sequences on the spectrum-luminosity diagram (see figure below) – and based on this class, determine its absolute magnitude. Once the absolute magnitude is known, the star’s mass can be calculated using the mass-luminosity relation (only stars within and outside of this relation do not adhere to it).
There is another technique for determining the mass of a star that involves measuring the gravitational redshift of its spectral lines in its gravitational field. In a gravitational field that is spherically symmetric, this is equivalent to the Doppler redshift, where M is the mass of the star in terms of solar mass units, R is the radius of the star in units of the Sun’s radius, and v r is expressed in km/s. This relationship has been tested on white dwarfs that are part of binary systems, where the radii, masses, and true orbital velocity projections are known.
There have been observations of invisible (dark) satellites near certain stars, detected through the observed oscillations of the star’s position as it moves near the common center of mass (see ). These satellites have masses less than 0.02 and are likely not self-luminous objects, but rather more similar to planets.
After analyzing the masses of stars, it was determined that their range is approximately from 0.03 to 60. The majority of stars fall within the mass range of 0.3 to 3. For comparison, the mass of stars in the vicinity of the Sun is about 10^33 g. While the difference in star masses is relatively small, their luminosities can vary greatly, reaching tens of millions. Additionally, stars differ significantly in terms of their radii. Consequently, their mean densities can vary greatly as well, ranging from a few up to several g/cm^3 (the mean density of the Sun is 1.4 g/cm^3).
When examining planets from a physical perspective, it is crucial to determine their size and mass. With this information, it becomes easy to calculate the average density of the planet.
The determination of planet masses with satellites is based on Kepler’s III law in its precise form. If M represents the mass of the Sun, m represents the masses of the planet and the satellite, T represents the periods of revolution of the planet around the Sun and the satellite around the planet, and a represents the major semi-axes of their orbits, then Kepler’s III law can be expressed as follows:
Due to the fact that the masses of the planets are significantly smaller than the mass of the Sun, and the masses of the satellites are typically negligible compared to the masses of the planets, we can disregard the second terms in parentheses and obtain the ratio of the planet’s mass to the mass of the Sun:
By knowing the mass of the Earth, we can utilize this formula to determine the mass of the Sun and subsequently the masses of those planets that possess satellites.
It is a challenging task to determine the masses of planets that do not have satellites, as well as the masses of satellites and asteroids themselves.
Originally, the masses of Mercury and Venus were calculated based on the disturbances they caused in the movement of other planets. However, thanks to spacecraft missions to these planets, we have been able to significantly improve the accuracy of their mass measurements by observing their effects on the spacecraft’s trajectory. Until recently, the mass of Pluto was only roughly known, but with the recent discovery of Pluto’s satellite, we have been able to refine its mass. The mass of the Moon has been determined by studying its influence on the Earth, which causes the Earth to orbit in a small ellipse around their common center of gravity. The masses of Jupiter’s large satellites can be determined by analyzing their mutual disturbances. As for other satellites and asteroids, we can only make approximate estimates of their mass and diameter based on their brightness (see § 7).
The size of a planet can be easily calculated by determining the distance and measuring its angular diameter. Because the angular diameters of planets are very small (less than 1), we can express this relationship as:
where is the distance of the planet from the Earth, d" is its angular diameter in seconds of arc, and D is its linear diameter.
Planets’ angular diameters are measured using a unique instrument called a micrometer, which is positioned at the center of the telescope. The most commonly used micrometer is a thread micrometer. Its design is as follows: two thin threads are fixed perpendicular to each other on a stationary frame. Along the frame, in alignment with the horizontal thread, another frame with a vertical thread parallel to the fixed vertical thread can be adjusted. The movement of this thread is achieved by using a micrometer screw, where each turn of the screw moves the frame by a precise amount, known as the screw pitch.
To determine the angular size of planets, the micrometer is rotated in such a way that the horizontal thread aligns with the measured diameter. This is necessary because the apparent diameters of planets, both polar and equatorial, can differ significantly due to their compression.
When using long-focus telescopes, the accuracy of these measurements can reach up to hundredths of a second of arc.
By using a thread micrometer, it is possible to measure not only the angular diameters of all planets with visible disks, but also their polar compression, phase magnitude, as well as the position of dark bands on Jupiter and the extent of polar caps on Mars, among other things.
The heliometer is another tool used to measure the angular diameters and phases of planets. It is a refractor telescope that has a split objective lens, with both halves able to slide along their common diameter using a micrometer screw. Additionally, the entire system can be rotated around the optical axis of the telescope.
When the two halves of the objective lens are extended, two images of the planet are seen in the eyepiece instead of one. By adjusting the micrometer screw, the two images can be brought into contact with each other. At this point, one of the images will be displaced relative to the other by the exact angular diameter of the planet. By knowing the amount of rotation produced by the heliometer screw and taking a reading, we can determine the desired value.
The heliometer is more complex than the thread micrometer because it requires special optics, unlike the latter which can be adapted to any telescope. Furthermore, the heliometer lens needs to be sawed, limiting its potential dimensions. However, the heliometer offers higher accuracy in measurements.
Photographic plates can also be used to measure the angular diameters of planets. In this case, specialized laboratory instruments are employed, including a table for placing the plate, two micrometer screws for adjusting its position in two perpendicular directions, and a microscope for examining the planetary disks, which can be very small at times.
To convert the measured values on the plate into angular units, knowledge of the image scale is necessary.
If the image is captured at the focal point of the objective lens, its scale is determined by the ratio
that is, 1″ on the image is equivalent to 1/206,265 of the focal length of the lens. For a lens with a focal length of 2m, this would be just 0.001mm, and for the longest refractor telescope at Yerkes Observatory, it would be approximately OD mm.
If photographing is done with additional magnification, such as using an eyepiece, it is necessary to ascertain the magnification factor of the system, i.e. to determine how much it enlarges the image. This value can be calculated using the formula
The distance from the plate when taking photographs is denoted by g, while the focal length of the eyepiece is represented by f. It is worth mentioning that capturing images of planets with a high magnification (greater than 10 times) is restricted by the decrease in image illumination (refer to section 6 for details).
Special optical systems are employed in serious work to magnify the image rather than using regular eyepieces. One such system is a concave (diffusing) lens, also known as a Barlow lens, which decreases the convergence angle of the rays. This effectively increases the focal length of the lens and, consequently, the size of the planet’s image. It is worth noting that the planetary disks captured in photographs are typically quite small. For instance, in 1909, G. A. Tikhov captured images of Mars using a 30-inch refractor at the Pulkovo Observatory (F=14 m), resulting in a planet image with a diameter of approximately 1.5 mm. However, with the use of a magnifying system, even such large telescopes can produce a Mars disk measuring 8-10 mm and a Jupiter disk of up to 15 mm.
Table 3 presents the angular diameters of the planets and certain satellites at their minimum and maximum distances from Earth.
For the largest refractor telescope in the world, the theoretical limit of measurement accuracy is the same, but in real observation conditions, it increases due to atmospheric turbulence and other distortions.
Therefore, according to Table 3, Pluto among the major planets, Triton among the satellites, and Juno among the minor planets are at the threshold of measurable angular diameters.
As mentioned earlier, in order to estimate the size of small or distant objects such as satellites and asteroids, we must rely on indirect methods, primarily photometric ones (see § 7).
What methods have scientists employed to determine the mass of the Earth and other planets?
When it comes to planets, their immense size makes it impossible to simply place them on a scale. Therefore, scientists have had to devise creative ways to determine the mass of the Earth and other celestial bodies. So how exactly have they accomplished this? Let’s take a closer look.
The intriguing world of physics
There are two primary methods used to determine the mass of the Earth: utilizing a barometer and employing mathematical calculations, or studying neutrino particles.
The barometer and Newton’s laws
This method has been employed since the 18th century. By applying Newton’s second law (F=mg) and the law of universal gravitation (F=G*m*M/R^2), scientists can accurately calculate the mass of the Earth.
In this equation, F represents the Earth’s gravitational force on the barometer, G is the gravitational constant coefficient, R is the radius of the planet, m is the weight of the instrument, and M is the weight of the planet.
To calculate the mass of the Earth, the following formula is used: M = g*R^2/G, where g represents the acceleration of free fall.
The acceleration of free fall was determined by dropping a barometer from a tall tower and measuring the time it took to reach the ground. It was found that the barometer traveled approximately 9.8 meters per second for each consecutive second. Thus, g = 9.8 m/s².
The radius of the Earth has been known since ancient times. This remarkable discovery was made by the Greek mathematician Eratosthenes in the 3rd century BC.
The scientist chose the day of the summer solstice for his experiment. During this time, the sun is at its highest point in the sky and at 12 o’clock, it casts the shortest shadow of the year.
The Earth is not a perfect sphere, so its radius was determined to be 6371 kilometers.
The most challenging task was to determine the coefficient of the gravitational constant. To accomplish this, the scientists used a one-ton lead ball and observed the force with which it attracted the barometer.
By plugging in these values into the equation, the researchers computed that the Earth has a weight of six septillion kilograms or 6^24 kg.
These are the minuscule subatomic particles emitted by the sun, which pass through the planet.
Spanish physicists established a laboratory at the South Pole, waited for the Sun to be at the North Pole, and captured the neutrinos from the opposite side.
The experiment may sound incredible, but by measuring the speed of the particles that traversed the Earth, the physicists determined the planet’s density and consequently its mass.
What is the method for measuring distant planets?
The measurement of distant planets is approximately calculated using various factors such as their orbits, the orbits of their satellites, and the gravitational disturbances between them.
The masses of stars, on the other hand, are determined by their brightness. It is commonly believed that the brighter a celestial body is, the more massive it tends to be. The luminosity of a star can provide valuable information about its chemical composition, approximate density, and weight.
Measuring the Mass of Planets
During the Middle Ages, when Kepler and Galileo were making their discoveries, scientists were already able to estimate the masses of planets using basic methods and instruments. Today, modern astronomy offers a variety of techniques for calculating the characteristics of planets, stars, clusters, and galaxies.
The solar system consists of various planets. It is worth noting that the majority of the mass, approximately 99.9%, is centralized in the Sun. The remaining 0.01% is distributed among the planets. Furthermore, within this small percentage, the gas giants hold the majority. Specifically, Jupiter and Saturn alone account for 90% of the mass among the gas giants.
To determine the mass of the planets in our solar system, the first step is to gather data for Earth. As we recall, the force of gravity can be calculated using the equation F=mg, where m represents the mass of an object and F is the force acting upon it.
Additionally, we must consider Newton’s law of universal gravitation:
By comparing these two equations and utilizing the known value for the gravitational constant (6.67430(15)-10-11 m³/(kg-c²)), we can calculate the mass of Earth. With the knowledge of Earth’s gravitational acceleration (9.8 m/s2) and the planet’s radius, we can input the data and obtain an approximate mass of 5.97 x 10²⁴ kg.

By knowing the mass of the Earth, we can easily determine the parameters of other celestial bodies in our solar system, such as the Moon, planets, and the Sun. Calculating the mass of the Moon is relatively straightforward. It involves considering that the distances from the centers of these bodies to the center of mass are inversely proportional to their masses. By substituting the relevant figures for the Earth and its satellite, we can determine that the mass of the Moon is 7.36 × 10²²² kilograms.
Now, let’s shift our focus to the methods used to measure the masses of the terrestrial planets – Mercury, Venus, and Mars. Afterwards, we will delve into the gas giants, and finally, explore exoplanets, stars, and galaxies.
Methods for Estimating Planetary Masses
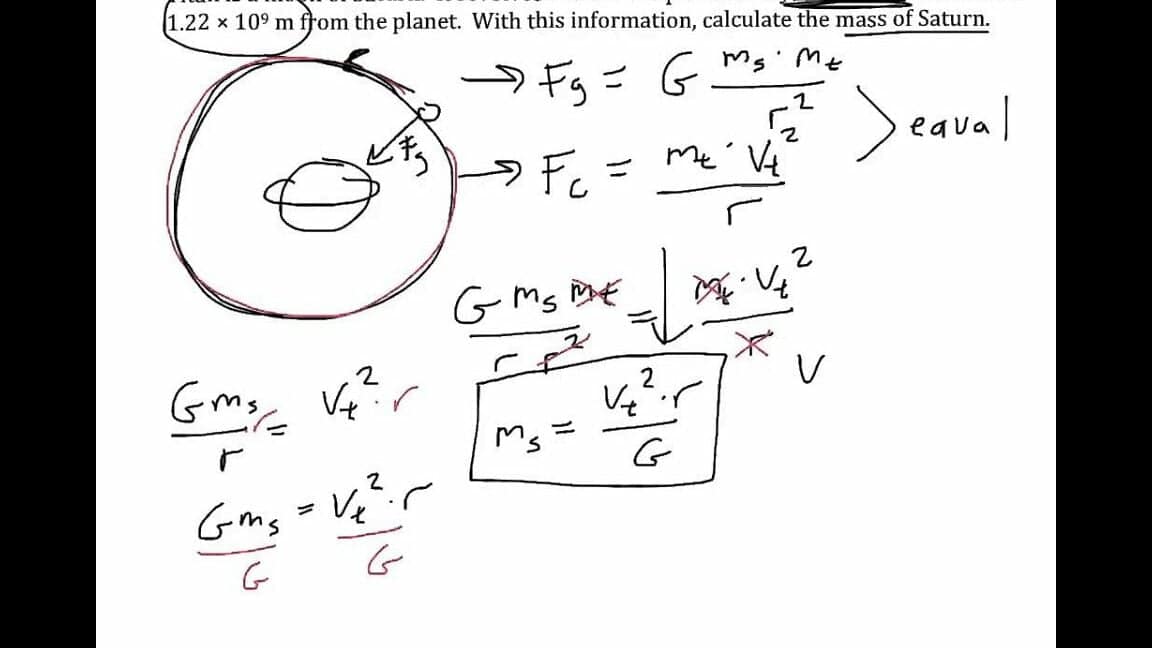
One common approach to determining the mass of a planet is to apply Kepler’s third law. This law establishes a relationship between the periods of a planet’s orbit and the lengths of its semi-major axis. Newton expanded upon this law by incorporating the masses of celestial bodies into the equation. The resulting formula is:
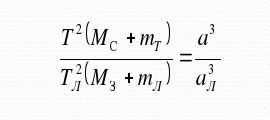
By utilizing astronomical techniques, we can determine the masses of all the planets in our Solar System, as well as the mass of the Sun. The periods of revolution and the major semi-major axes of the planets’ orbits can be easily measured using basic astronomical methods, even without the need for advanced instruments. With the Earth’s mass already calculated, we can input all the values into the formula and obtain the final result.
When it comes to exoplanets and double stars, astronomy typically employs a method that involves analyzing visible perturbations and oscillations. This method is based on the fact that massive bodies have an impact on each other’s orbits.
The Masses of Planets in the Solar System
Having discussed the general methods for calculating the masses of various celestial bodies and determining the values for the Moon, Earth, and the Galaxy, it is now time to rank the planets in our solar system based on their masses.
Topping the list with the largest mass among the planets in the solar system is Jupiter, which falls just short of doubling the mass of our system by one order of magnitude. If Jupiter were to replace our second sun, we would have a binary star system. The mass of this gas giant is 1.9 × 10²⁷ kilograms.
Interestingly, Jupiter is the only planet in our solar system whose center of mass, in terms of its rotation with the Sun, lies outside of the star’s surface. It is located about 7% of the distance between the surface of Jupiter and the surface of the Sun.
The planet with the second highest mass is Saturn, weighing approximately 5.7 × 10²⁶ kg. Following Saturn is Neptune, which has a mass of 1 × 10²⁶ kg. Uranus, the fourth most massive planet, is a gas giant and has a mass of 8.7 × 10²⁵ kg.
After the gas giants, we have the terrestrial group planets, which are rocky bodies and differ from the gas giants in terms of their larger radius and relatively lower density.

The most massive planet in our solar system has already been determined, and it is our planet. Moving on to Venus, it has a mass of 4.9 × 10²⁴ kg. Following Venus is Mars, which is nearly ten times lighter, weighing in at 6.4 × 10²³ kg. Lastly, we have the planet with the smallest mass, Mercury, which weighs 3.3 × 10²³ kg. Interestingly, Mercury is even lighter than two of the satellites in our solar system, Ganymede and Callisto.
Determining the masses of stars and galaxies
The gravimetric method is employed to determine the characteristics of individual star systems. This method involves measuring the gravitational redshift of the star’s light. The redshift can be calculated using the formula ∆V=0.635 M/R, where M and R represent the mass and radius of the star, respectively.
Additionally, the mass of a star can be indirectly estimated by analyzing its visible spectrum and luminosity. The luminosity class of the star is first identified using the Hertzsprung-Russell diagram, followed by the calculation of the mass/luminosity relation. It should be noted that this method is not applicable to white dwarfs and neutron stars.
On this occasion, we substitute the measurement from the Sun to the heart of our galaxy and its mass into the equation. This is how we can compute the mass of the Milky Way, which amounts to 2.2 × 10⁴⁴⁴g.
We must remember that this value represents the mass of the galaxy without considering the stars whose orbits are positioned beyond the orbit of the Sun’s rotation. Consequently, for more precise computations, the outermost stars of the arms of spiral galaxies are included.
Regarding elliptical galaxies, the approach for determining the mass is analogous, except that in this case, the connection between the angular size, the velocity of stars, and the total mass is taken into account.
Enjoyed reading this article? Don’t hesitate to share it with your friends!

Therefore, the Sun’s mass is 300,000 times greater than that of the Earth. Calculating the average density of the Sun is a simple task: divide its mass by its volume. This reveals that the Sun’s density is approximately one-fourth that of the Earth.
When it comes to determining the mass of the Moon, one astronomer stated, “Despite being closer to us than any other celestial body, it is more challenging to measure its weight than that of Neptune, the most distant planet at the time.” Unlike the Sun, the Moon lacks a companion to aid in mass calculation. Scientists had to employ alternative, more intricate methods, one of which we will briefly discuss. This method involves comparing the height of the tides caused by the Sun and the Moon.
The height of the tide is influenced by the mass and distance of the celestial body causing it. By knowing the mass and distance of the Sun and the distance of the Moon, we can determine the mass of the Moon by comparing the heights of the tides. This calculation will be discussed later when discussing tides. For now, let’s focus on the final result: the mass of the Moon is 1/81 of the mass of the Earth (Fig. 89).
Once we have the diameter of the Moon, we can calculate its volume, which is found to be 49 times smaller than the volume of the Earth. Therefore, the average density of our satellite is 49/81 = 0.6 times the density of the Earth.
Figure 89. The Earth “weighs” 81 times more than the Moon.
Therefore, the Moon is made up of a substance that is more fragile than the Earth on average, but it is denser than the Sun. Moving forward, we will observe (refer to the table on page 199) that the mean density of the Moon surpasses the mean density of most planets.
Planets and Stars: Weight and Density
The method used to determine the Sun’s weight can also be applied to determining the weight of any planet that has at least one satellite.
By knowing the average velocity v of the satellite’s orbit and its average distance D from the planet, we can set the centripetal force that keeps the satellite in its orbit, mv 2 /D, equal to the force of gravitational attraction between the satellite and the planet, which is kmM/D 2 . Here, к – represents the force of attraction of 1 g to 1 g at a distance of 1 cm, m – is the mass of the satellite, and М – is the mass of the planet:
By utilizing this equation, it becomes a simple task to compute the mass M of the celestial body.
Furthermore, Kepler’s third law can be applied in this scenario:
By disregarding the negligible terms within the parentheses, we can derive the ratio between the mass of the Sun and the mass of the celestial body.
Once we possess knowledge of the Sun’s mass, determining the mass of the celestial body becomes a straightforward process.
The same calculation can be employed for binary stars, except the outcome of the calculation represents the combined mass of the stellar pair rather than the individual masses of the stars.
However, ascertaining the masses of planet satellites, as well as planets without any satellites, presents a significantly greater challenge.
When it comes to asteroids, their mass is so insignificant that it doesn’t have any noticeable effect on each other, making it generally impossible to determine their mass. We can only make guesses about the total mass of all these small planets.
By knowing the mass and volume of the planets, we can easily calculate their average density. The results are shown in the table below:
From the table, we can see that Earth and Venus are the densest planets in our solar system. The lower average densities of the larger planets can be explained by the fact that each of them has a solid core covered by a massive atmosphere, which adds to the apparent volume of the planet but doesn’t contribute much to its mass.
Gravity on the Moon and Other Planets
Many people who are not familiar with astronomy often find it surprising that scientists can confidently discuss the gravity on the surfaces of the Moon and other planets, despite never having been there. However, it is actually quite simple to calculate the weight of a kettlebell on other celestial bodies. All that is required is knowledge of the radius and mass of the specific celestial body.
Let’s calculate the gravitational force on the Moon, for instance. The Moon’s mass is 81 times smaller than the Earth’s mass. If the Earth had such a reduced mass, the gravitational force on its surface would be 81 times weaker than it currently is. However, according to Newton’s law, an object attracts as if all of its mass were concentrated at its center. The center of the Earth is at a distance equal to its radius from its surface, while the center of the Moon is at a distance equal to the lunar radius. However, the lunar radius is 27/100 of the Earth’s radius, and by reducing the distance by a factor of 100/27, the gravitational force increases by a factor of (100/27) 2. Therefore, the actual gravitational force on the surface of the Moon is
So, if a 1 kilogram weight is taken to the surface
On the moon, an object would have a weight that is only 1/6 of its weight on Earth. However, this decrease in weight can only be measured using spring scales, not lever scales (Fig. 90).
Figure 90. The difference in weight of a man on various planets. The weight of a man on Pluto is not 18 kg, but only 3.6 kg (according to current data)
Interestingly, if there was water on the Moon, a swimmer would feel the same in a lunar body of water as they do on Earth. Their weight would be reduced by six times, but the weight of the water displaced by them would also be reduced by the same ratio. This means that the swimmer would be immersed in the water of the Moon in the same way as they are immersed in our water on Earth.
Displayed below is a comparison table of the gravitational force on various planets in relation to Earth’s gravity.
The table illustrates that Earth ranks fifth in terms of gravity among all the planets in our solar system, following Jupiter, Neptune, Saturn, and Uranus.[51] Earth’s gravitational force is placed fifth among all the planets in our solar system, following Jupiter, Neptune, Saturn, and Uranus. 51
For those interested in delving deeper into the study of gravity’s effects in the universe, Y.A. Ryabov’s book “The Movements of Celestial Bodies,” 2nd edition, published by Fizmatgiz in 1962, provides a wealth of fascinating information.
Recording the force of gravity
The force of gravity is at its highest level on the surface of “white dwarf” stars like Sirius B, which we discussed in Chapter IV. It is evident that the immense mass of these celestial bodies, combined with their relatively small radius, creates a significant gravitational strain on their surface. Let’s perform a calculation for a star in the Cassiopeia constellation, which has a mass 2.8 times that of our Sun and a radius half the size of Earth’s. Considering that the Sun’s mass is 330,000 times greater than Earth’s, we determine that the force of gravity on the surface of this star surpasses that of Earth’s by
2.8 – 330,000 – 2 2 = 3,700,000 times.
On Earth, 1 cm3 of water weighs 1 g. However, if we were to consider the substance of a star, which is 36,000,000,000 times denser than water, the weight would be astronomical.
In fact, 1 cm3 of this star substance would weigh approximately 3 3/4 т, which is equivalent to 133,200,000,000,000 г.
The concept of a thimbleful of matter weighing a hundred million tons is mind-boggling and was not even imagined by the most daring fiction writers until recently.
Gravity in the depths of planets
What happens to the weight of an object when it is taken deep into a planet, like the bottom of an incredibly deep mine?
Many people mistakenly think that the body would become heavier at the bottom of such a mine. After all, it is closer to the center of the planet, where all objects are attracted. However, this thinking is incorrect. The force of attraction towards the center of the planet does not increase at depth, but actually weakens. I have explained this concept in a more understandable way in my book “Entertaining Physics”. So, to avoid repeating what was already discussed there, I will just mention the following points.
Figure 91. A body inside a ball shell experiences zero weight
Fig. 92. What determines the weight of a body inside a planet?
Fig. 93. Calculating the change in weight of a body as it approaches the center of a planet
Based on these principles, it is not difficult to derive the law that governs how the weight of a body changes as it approaches the center of a planet. Let’s denote the radius of the planet (Fig. 93) as R and the distance of the body from its center as r. The gravitational force on the body at this point must increase by a factor of (R/r) 2 and simultaneously weaken by a factor of (R/r) 3 (since the planet’s gravitational pull has decreased by the specified amount). Eventually, the gravitational force must weaken.
Therefore, as one delves into the depths of a planet, the body’s weight should decrease proportionally to the distance from the center of the planet. For instance, on a planet the size of Earth, with a radius of 6400 km, descending to a depth of 3200 km would result in a weight reduction of half, while descending to 5600 km would result in a weight reduction of
At the very core of the planet, the body’s weight would be completely lost, as the planet’s weight is reduced by half.
However, it is possible to predict this outcome without performing calculations, as the body at the core of the planet is equally pulled towards the surrounding matter from all directions. These thoughts are relevant to a hypothetical planet that has a uniform density. They can only be partially applied to actual planets. Specifically, for a planet with a greater density at its core compared to its surface, the gravitational force near the center deviates slightly from the established pattern: it initially increases to a certain depth (albeit to a relatively small extent) and then starts to decrease as the depth increases.
Lunar and solar tides
It should not be assumed that a tidal wave is caused solely by the Moon or the Sun exerting a direct pull on the water. The Moon’s gravitational pull affects not only the water on the Earth’s surface, but the entire planet. However, the gravitational attraction originates from a point that is further from the center of the Earth than the water particles on the surface that are facing the Moon. At the zenith point where the Moon is located, each kilogram of water is attracted by it with a force that is 2kMr/D 3 stronger than the force exerted by a kilogram of the Earth’s core substance. Conversely, the water at the opposite point on the Earth is attracted with a force that is weaker by the same amount.
The effect on the ocean waters and the gravitational pull of the Sun are similar, but which one is more powerful: the Sun’s or the Moon’s? Comparing their direct gravitational pull, it seems that the Sun’s pull is stronger. This is because the Sun’s mass is 330,000 times greater than that of the Earth, while the Moon’s mass is 81 times smaller, meaning it is 330,000 x 81 times smaller than the Sun’s mass. The distance from the Sun to the Earth is 23,400 Earth radii, while the distance from the Moon to the Earth is 60 Earth radii. Therefore, the attraction of the Earth by the Sun is proportional to the attraction of the Earth by the Moon as
Therefore, the Moon’s gravitational pull on earthly objects is 170 times weaker than that of the Sun. This might lead one to believe that the solar tides are higher than the lunar tides. However, the reality is quite the opposite: the lunar tides are actually greater than the solar tides. If we denote the Sun’s mass as M, the Moon’s mass as M, the distance to the Sun as D, and the distance to the Moon as D, then the ratio of tidal forces between the Sun and the Moon is equal to
Let’s assume that the Moon’s mass is known: 1/81 – the mass of the Earth.
Given this, and the fact that the Sun is 400 times farther from the Moon, we can conclude that the tides generated by the Sun must be approximately 2 1/2 times lower than the lunar tides.
Here it is appropriate to demonstrate how the mass of the Moon was determined by comparing the heights of the lunar and solar tides. It is not possible to observe the height of each tide separately as the Sun and the Moon always act together. However, it is possible to measure the tide height when the effects of both celestial bodies are combined (i.e. when the Moon and the Sun are aligned with the Earth), and when their effects are opposite (the line connecting the Sun to the Earth is perpendicular to the line connecting the Moon to the Earth). Observations have revealed that the second tides are 0.42 times the height of the first tides. If the tidal force of the Moon is represented by x and that of the Sun by y, then
Therefore, based on the previously derived formula:
Given that the mass of the Sun Ms is equal to 330,000 times the mass of the Earth Me, we can easily determine that the mass of the Moon is a fraction of the Earth’s mass. A more precise calculation yields a value of 0.0123 times the mass of the Earth. This calculation is based on measurements of periodic variations in the longitudes of the planets and the Sun, which are caused by the motion of the Earth and the Moon around their center of mass, known as the barycenter.
The Impact of the Moon on Weather
There is a widespread interest in understanding how the tides generated by the Moon affect atmospheric pressure in our planet’s air ocean. These tides were first discovered by the renowned Russian scientist M.V. Lomonosov, who referred to them as air waves. While many researchers have studied these tides, there are still common misconceptions about their influence. Non-experts often imagine that the Moon creates massive tidal waves in the Earth’s light and mobile atmosphere. This leads to the belief that these tides have a significant impact on atmospheric pressure and should play a decisive role in meteorology.
Remember the school experiment with an empty tube, where a lead ball, when dropped, does not form a clump. The tidal phenomenon is ultimately caused by nothing other than the descent of the globe and its lighter layers in the world’s space due to the gravitational pull of the Moon (and the Sun). In the empty expanse of space, all objects – whether heavy or light – fall at the same rate and experience the same displacement from the gravitational force, as long as their distance from the center of attraction is equal.
This concept prepares us for the notion that the magnitude of atmospheric tides must be equivalent to those in the ocean, particularly in areas far away from land. In fact, if we were to examine the formula used to calculate the height of tides, we would observe that it solely relies on the masses of the Moon and Earth, the radius of the planet, and the distance between the Earth and Moon. Neither the density of the fluid being lifted nor the depth of the ocean play a role in this equation. By substituting the water ocean with the air ocean, we do not alter the outcome of the calculations, resulting in the same height for atmospheric tides as those in the ocean. Furthermore, the latter value is quite insignificant. The theoretical height of the highest tide in the open ocean is approximately ½ m, but only the contours of the shores and the ocean floor, which restrict the tidal wave, elevate it to 10 m or even higher in certain locations. Intriguing devices exist for forecasting the height of tides at a specific location and time based on data regarding the positions of the Sun and Moon.
Within the vast expanse of the atmosphere, nothing has the power to disrupt the theoretical model of lunar tides and alter their maximum theoretical height, which is half a meter. This minimal increase can only have an insignificant impact on atmospheric pressure.
Laplace, a researcher of air tides, concluded that the fluctuations in atmospheric pressure caused by lunar tides should not exceed 0.6 mm of mercury, and the winds generated by these atmospheric tides do not exceed a speed of 7.5 cm/s.
It is evident that atmospheric tides do not play a significant role among the various weather factors.
These considerations render baseless the attempts made by various “lunar prophets” to predict the weather based on the Moon’s position in the sky.
Is there a way to determine the weight (or more accurately, the mass) of the Sun, considering the immense size of our “home star” that is beyond our understanding? It seems like there might be a hidden solution… And while you may be both correct and mistaken in your thinking.

Initially, the concept of determining the weight of the Sun may appear incredible. However, it actually requires nothing more than basic calculations.
On one hand, there is no mystery to measuring the weight of any celestial body, regardless of its size. On the other hand, certain techniques are undoubtedly necessary in this case.
Let’s put it this way: when we refer to “determining the weight of the Sun,” we are essentially referring to “determining the quantity of matter that comprises the Sun.”
First and foremost, let’s determine the Earth’s mass.
By rephrasing the problem in this manner, we will promptly uncover the hints that lead to the solution. The initial step is to ascertain the magnitude of the gravitational force between any two masses.
The procedure for this determination is as follows:
Imagine an incredibly sensitive and delicately balanced scale with two cups. Each cup (A and B) holds an identical weight, with the same mass. In this scenario, the scale will be perfectly balanced.
Now, let’s introduce a third body (B) with a known mass and place it beneath A. The expected mutual attraction between A and B causes cup A to tilt downward. To restore equilibrium, we need to add a very small, but still measurable mass G to body B.
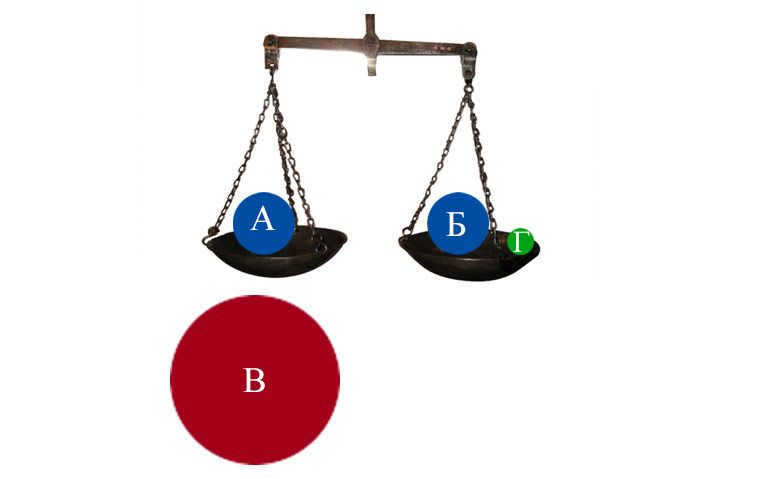
What is the method for calculating the weight of planet Earth without leaving your house?
Now comes the intriguing part: given that the force of attraction exerted by the entirety of Earth on object G equals the mutual attraction between A and B, it is a simple task to ascertain the weight of Earth, which amounts to 6.59 x 10 21 tons..
Now we will determine the weight of the Sun!
The Earth, as it orbits, behaves as if there is an imperceptible thread connecting it to the Sun. In fact, the gravitational pull can be likened to the tension in a thread, causing the Earth to continue moving towards the Sun instead of veering off in a straight line, which would occur if this “thread” were to suddenly snap. It can be said that while orbiting the Sun, the Earth is in a perpetual state of “falling” towards it.
Therefore, by taking into account the fact that the force of gravity exerted by an object is directly proportional to its mass and inversely proportional to the square of the distance from the center of the object, we can easily determine that the mass of the Sun is 329,390 times greater than the mass of the Earth..
By utilizing the aforementioned value of the Earth’s mass, we can deduce that the mass of the Sun is equivalent to 2.24 x 10 27 tons. In its entirety, this unfathomable quantity can be expressed as 2,240,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000 tons.
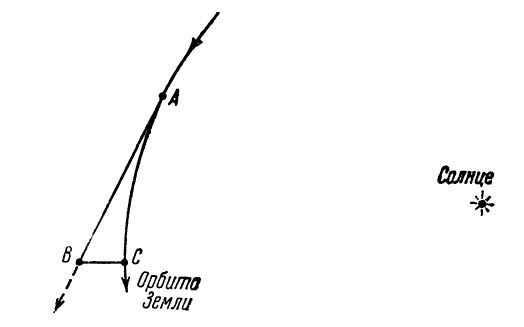
The impact of gravity on the movement of the Earth. The trajectory A-C represents the path that the Earth covers along its orbit in one second (30 km), and the deviation from the straight line B-C will only be 3 millimeters.
Now we can determine the average density of the Sun, which is its mass divided by the mass of water that occupies the same volume.
Since one cubic centimeter of water weighs one gram, we simply need to divide the mass of the Sun (in grams) by its volume (in cubic centimeters). The resulting value is 1.42.
In other words, on average, a certain volume of solar matter should weigh approximately the same as a lump of bituminous coal occupying the same volume.
By nature, the “mean value” is the average value that represents a sort of middle ground between the core of the sun (where the density of matter is 10 times greater than steel) and the matter of the sun’s corona (where the density almost equals that of the cosmic vacuum). However, overall, this calculation method is entirely accurate and can be effectively utilized to determine the mass of any celestial object – be it an asteroid or a star.
uCrazy.ru
Navigation
BEST OF THE WEEK
QUESTION
NOW ON THE SITE
CALENDAR
Today is a birthday
Recommended
How do scientists determine the mass of the Earth and other planets?
Planets are massive objects that cannot be placed on a scale. So how do scientists go about measuring the mass of the Earth? How is the mass of distant celestial bodies calculated?
There are two methods for determining the mass of the Earth: using a barometer and mathematical calculations, or analyzing neutrino particles.
The barometer and Newton’s laws
This method has been used since the 18th century. Newton’s second law (F=mg) and the law of universal gravitation (F=G*m*M/R^2) are employed in the calculations.
To calculate the mass of the Earth, the following formula is used: M = g*R^2/G, where g represents the acceleration due to gravity.
The acceleration due to gravity was determined by conducting an experiment where a barometer was dropped from a tall tower and the time it took to reach the ground was measured. It was found that the barometer traveled approximately 9.8 meters per second for each successive second. Therefore, g = 9.8 m/s².
The radius of the Earth has been known since ancient times. This significant discovery was made by the Greek mathematician Eratosthenes in the 3rd century BC.
The scientist chose the day of the summer solstice to conduct his experiment. During this time, the sun is at its highest point in the sky and at 12 o’clock it casts the shortest shadow of the year.
The mathematician carefully examined a nearby obelisk, measuring both its shadow and height, and calculating the angles involved. This process was repeated in a neighboring town. The resulting calculations yielded an Earth circumference of 38.5 thousand kilometers. In modern times, scientists have recalculated the circumference using a similar method and arrived at a measurement of 40,000 kilometers.
It is important to note that the Earth is not a perfect sphere, leading to a calculated radius of 6371 km.
The most challenging aspect of this research was determining the gravitational constant coefficient. To accomplish this, the researchers utilized a one-ton lead ball and observed the force with which it attracted a barometer.
By plugging these various numbers into an equation, the scientists were able to calculate that the Earth has a weight of six septillion kilograms or 6^24 kg.
These subatomic particles that the Sun emits are extremely small. They have the ability to travel through the entire planet without any obstacles.
A group of physicists from Spain decided to conduct an experiment at the South Pole. They patiently waited for the Sun to be positioned at the North Pole and successfully managed to capture the neutrinos as they passed through the back side of the planet.
Although the experiment may sound incredible, the physicists were able to determine the planet’s density and mass by measuring the speed of the particles that traveled through the Earth.
How do scientists measure the mass of distant planets?
The mass of distant planets is typically estimated in an approximate manner. Scientists base their calculations on factors such as the planets’ orbits, the orbits of their satellites, and the gravitational disturbances that occur between them.
The mass of stars can be determined by their level of brightness. It is commonly believed that the more luminous a celestial body is, the more mass it has. The brightness of a star is an indicator of its chemical composition, which in turn provides an estimate of its density and weight.
Mass of planets – Planetary mass
Planetary mass refers to the mass of an object that resembles a planet. In the solar system, planets are typically measured using astronomical units, with the mass of the Sun ( M ☉ ) serving as the unit of mass. When studying exoplanets, the mass of Jupiter ( M J ) is commonly used as the unit of measurement for large gas giant planets, while the mass of the Earth ( M ⊕ ) is used for smaller rocky terrestrial planets.
The mass of a planet in the solar system is a parameter that can be customized when preparing ephemerides. There are three options for determining the planetary mass:
- If a planet has natural satellites, its mass can be calculated using Newton’s law of universal gravitation to derive Kepler’s third law, which takes into account the masses of the planet and its moons. This method was used to measure Jupiter’s mass in solar mass units.
- The mass of a planet can be inferred from its influence on the orbits of other planets. However, in the period of 1931-1948, incorrect applications of this method led to inaccurate calculations of Pluto’s mass.
- Data collected from the orbits of space probes can also be used to determine the mass of a planet. Examples include the Voyager probes sent to the outer planets and the MESSENGER spacecraft sent to Mercury.
Choice of units
The choice of solar mass, M☉, as the fundamental unit for planetary mass arises directly from the calculations employed in determining planetary mass. In the most precise scenario, the mass of the Earth itself is expressed in solar mass units with a precision of twelve significant figures. In contrast, the mass in kilograms or other units based on Earth is known with only five significant figures, which are less accurate by a factor of less than one millionth.
The distinction lies in how the masses of celestial bodies are determined. Measuring the weight of a planet or the Sun using standard laboratory weight measurements is not feasible. However, the positions of planets in their orbits provide a wealth of observational data, which can be used to compare their relative masses according to Newton’s law of universal gravitation (with slight adjustments for general relativity when necessary). To convert these relative masses into units such as kilograms, it is necessary to know the value of Newton’s gravitational constant, G. Measuring this constant in practice is extremely challenging, and its value is currently known only to the closest ten-thousandth.
The Sun has a mass of 1.9884 (2) × 10 30 kg, which is a significantly large unit in the solar system. Comparatively, Jupiter, the largest planet, only has a mass that is 0.09% of the Sun’s mass, while the Earth’s mass is even smaller at about 0.0003% of the Sun’s mass. To address this issue, various conventions have been employed in literature. One approach is to invert the ratio to express a planet’s mass in terms of how many planets would be needed to form one Sun. In this case, we have chosen to present all planetary masses in “microSuns”. For example, the mass of the Earth is slightly over three “microSuns”, which is equivalent to three millionths of the Sun’s mass, unless otherwise specified in kilograms.
When making comparisons between planets, it is frequently advantageous to utilize the Earth’s mass ( MЕ or M⊕ ) as a reference point, especially for terrestrial planets. On the other hand, when examining gas giants, as well as the majority of extrasolar planets and brown dwarfs, it is more convenient to compare their mass to that of Jupiter ( MJ ).

The mass of a planet has implications for its structure due to its significant mass, particularly during its formation process. If a celestial body has a mass greater than one ten thousandth of Earth’s mass, it can surpass its compressive strength and achieve hydrostatic equilibrium. As a result, it will adopt a roughly spherical shape. Since 2006, such celestial bodies have been categorized as dwarf planets if they orbit the Sun, unless they are satellites of another planet. Smaller bodies like asteroids are referred to as “small solar system bodies.”
By definition, a dwarf planet lacks the gravitational force necessary to clear its neighboring region of planetesimals. The exact mass required for a planet to effectively cleanse its surroundings remains uncertain, but it is certain that one tenth the mass of Earth is sufficient.
The smaller celestial bodies consist solely of silicate materials and are classified as terrestrial planets, such as Earth or Mars. However, there are also multiple super-Earths with a mass less than that of Earth, denoted as ME. The internal structure of rocky planets is influenced by their mass, as plate tectonics, for instance, requires a minimum mass to generate the necessary temperatures and pressures.
If a protoplanet undergoes accretion and grows to a mass exceeding 5-10 M⊕, its gravitational force would become strong enough to retain hydrogen in its atmosphere. Consequently, it would transform into a gas giant. Should the planet then undergo migration, it could move within the frost line of its planetary system and eventually become a hot Jupiter, orbiting in close proximity to its host star. Over time, the star’s radiation would cause the hot Jupiter to gradually lose a small portion of its mass as its atmosphere is torn apart.
The estimated minimum mass of a star, capable of undergoing hydrogen fusion in its core, is approximately 75 MJ. However, deuterium fusion can occur at masses as low as 13 Jupiters.
Data from DE405 Ephemeris
The DE405 / LE405 ephemerides, developed by the Jet Propulsion Laboratory in 1998, provide comprehensive and widely used data for the entire solar system. These ephemerides ensure a consistent set of planetary masses, which may not always be the case with more recent data (refer to the information below).
| Mercury | 0. 166 01 | 3.301 × 10 23 kg | 5.43 g / cm 3 | ||
| Venus | 2. 447 8383 | 4.867 × 10 24 kg | 5.24 g / cm 3 | ||
| Earth/Moon system | 3 040 432 633 33 | 6.046 × 10 24 kg | 4.4309 g / cm 3 | ||
| earth | 3. 003 489 596 32 | 5.972 × 10 24 kg | 5.514 g / cm 3 | ||
| moon | 1. 230 003 83 × 10 −2 | 7.348 × 10 22 kg | 3.344 g / cm 3 | ||
| Mars | 0,3227151 | 6.417 × 10 23 kg | 3.91 g / cm 3 | ||
| Jupiter | 954,79194 | 1.899 × 10 27 kg | 1.24 g / cm 3 | ||
| Io | 4,70 × 10 −5 | 8.93 × 10 22 kg | |||
| Europa | 2,53 × 10 −5 | 4.80 × 10 22 kg | |||
| Ganymede | 7,80 × 10 −5 | 1.48 × 10 23 kg | |||
| Callisto | 5,67 × 10 −5 | 1.08 × 10 23 kg | |||
| Saturn | 285,8860 | 5.685 × 10 26 kg | 0.62 g / cm 3 | ||
| Titan | 2,37 × 10 −4 | 1.35 × 10 23 kg | |||
| Uranus | 43,66244 | 8.682 × 10 25 kg | 1.24 g / cm 3 | ||
| Titania | 4,06 × 10 −5 | 3.52 × 10 21 kg | |||
| Oberon | 3,47 × 10 −5 | 3.01 × 10 21 kg | |||
| Neptune | 51,51389 | 1.024 × 10 26 kg | 1.61 g / cm 3 | ||
| Triton | 2,09 × 10 −4 | 2.14 × 10 22 kg | |||
| Pluto / Charon system | 0,007396 | 1.471 × 10 22 kg | 2.06 g / cm 3 | ||
| Ceres | 0,00047 | 9.3 × 10 20 kg | |||
| Vesta | 0,00013 | 2.6 × 10 20 kg | |||
| Pallada | 0,00010 | 2.0 × 10 20 kg | |||
If a planet possesses natural satellites, the mass is typically given for the entire system (planet + satellites) because the mass of the entire system causes a disturbance in the orbits of other planets. The distinction is quite minor as natural satellites are much smaller in size compared to their parent planets (as shown in the table above, which only lists the largest satellites).
The Earth and the Moon serve as examples, partly due to the Moon’s unusually large size (slightly over 1% of the Earth’s mass) in relation to its parent planet and other natural satellites. Moreover, there is highly precise data accessible for the Earth-Moon system, particularly from the Lunar Laser Locator (LLR) experiment.
The geocentric gravitational constant, which is the result of multiplying the mass of the Earth by the Newtonian gravitational constant, can be measured with great precision by studying the orbits of the Moon and man-made satellites. The relative masses of these celestial bodies can be ascertained by observing the slight deviation in the Earth’s orbit caused by the gravitational force exerted by the Moon.
Latest data
Developing comprehensive and highly accurate ephemerides for the solar system is a challenging endeavor. It is possible (and somewhat less complicated) to create partial ephemerides that focus solely on the planets (or dwarf planets, satellites, asteroids) of interest by “fixing” the movement of the other planets in the model. These two approaches are not entirely equivalent, especially when it comes to determining the uncertainties of the outcomes. Nevertheless, the most reliable estimates – particularly in terms of the stated uncertainties in the findings – for the masses of minor planets and asteroids are typically derived from partial ephemerides.
Despite this, there are ongoing efforts to create fresh and comprehensive ephemerides, with the most prominent being the EPM2004 ephemeris developed by the Institute of Applied Astronomy of the Russian Academy of Sciences. The EPM2004 ephemeris is derived from an extensive set of 317,014 individual observations spanning the period from 1913 to 2003, which is more than seven times the number used for the DE405 ephemeris. Furthermore, the EPM2004 ephemeris provides more precise measurements of the masses of Ceres and five other asteroids.
In August 2009, the 27th General Assembly of the International Astronomical Union (IAU) gave its approval to a fresh collection of “current best estimates” for a range of astronomical constants.
| Mercury | 6023.6 (3) × 10 3 | 0.166014 (8) | 3.30 × 10 (3) × 10 23 |
| Venus | 408523719 (8) × 10 3 | 2081062.72 (3) | 4.1380 (4) × 10 24 |
| Mars | 3098.70359 (2) × 10 3 | 0.3232371722 (21) | 6.4273 (6) × 10 23 |
| Jupiter | 10473486 (17) × 10 3 | 9547919 (15) | 1.89852 (19) × 10 27 |
| Saturn | 3.4979018 (1) × 10 3 | 285.885670 (8) | 5.6846 (6) × 10 26 |
| Uranus | 22.90298 (3) × 10 3 | 43.66244 (6) | 8.6819 (9) × 10 25 |
| Neptune | 19.41226 (3) × 10 3 | 51.51384 (8) | 1.02431 (10) × 10 26 |
Latest IAU Estimates (2012)
The most recent “best estimates” as of 2012 were released by Resolution B2 of the XXVIII IAU General Assembly, updating the 2009 set. Notable improvements were made to the values for Mercury and Uranus, in addition to the Pluto and Vesta systems.
Our Planet © 2023
The content provided on this website is solely for informational purposes.

Since 2005, the consensus has been that there are eight planets in our solar system. This conclusion was reached after the discovery made by M. Browne, who provided evidence that Pluto is a dwarf planet. Naturally, there is a division of opinions among scientists: some argue that Pluto should not be deemed a dwarf planet and should regain its former classification, while others support Michael’s findings. There are even suggestions to expand the number of planets to twelve. Due to these conflicting perspectives, scientists had to establish criteria for classifying celestial objects as planets:
- They must orbit the Sun.
- Their mass must be sufficient to give them the gravitational force necessary to maintain a spherical shape.
- They must clear their orbital path of any additional objects.
Mercury
Mercury, the first and closest planet to the Sun, is located just 58 million kilometers away from it. It is known for being the smallest planet in our solar system, with a diameter of only slightly over 4800 kilometers. In terms of Earth’s time, one year on Mercury is equivalent to eighty-seven days, while one day on the planet lasts fifty-nine days. The mass of Mercury is only 0.055 times that of Earth, which amounts to 3.3011 x 10^23 kg.
The surface of Mercury bears a resemblance to the Moon, and interestingly, this planet does not have any satellites.
If an individual weighs fifty kilograms on Earth, their weight on Mercury will be around twenty kilograms. The temperature on Mercury can range from -170 to +400 degrees Celsius.
Venus
Venus, the second planet from the sun, is located approximately 108 million kilometers away. Although it is similar in diameter and mass to Earth, it is slightly smaller. With a mass of 4.886 x 10^24 kg, Venus is approximately 0.81 times the mass of Earth. A year on Venus lasts 225 days. The planet has a unique atmosphere composed of sulfuric acid, nitrogen, and carbon dioxide.
Due to its bright glow, Venus is often mistaken for a UFO and can be easily observed from Earth during the evening and morning hours.

Planet Earth
Our planet is situated at a distance of approximately 150 million kilometers from the sun. It has a mass of 5.97 x 10 24 kg. The Earth completes one orbit around the sun in 365 days. The temperature on our planet’s surface can range from +60 to -90 degrees Celsius. The Earth’s surface is constantly changing, with the percentage of land and water fluctuating over time. Additionally, we have a natural satellite known as the Moon.
Earth’s atmosphere mainly consists of nitrogen, oxygen, and other impurities. Scientists believe that Earth is the only planet in the solar system that supports life.
Mars
Mars, also known as the Red Planet, is situated almost three hundred million kilometers away from the Sun. The distinct reddish hue of its surface is caused by iron oxide. Mars shares similarities with Earth in terms of its axis of inclination and rotation, resulting in the formation of seasons on the planet.
The surface of Mars is adorned with numerous deserts, volcanoes, ice caps, mountains, and valleys. Its atmosphere is extremely thin, with temperatures plummeting to -65 degrees Celsius. In the solar system, Mars has a mass of 6.4171 x 10 24 kg. It takes the planet 687 Earth days to complete a revolution around the Sun, which means that if we were Martians, our age would be only half of what it is on Earth.
Recent data suggests that due to its mass and size, Mars is now classified as an Earth-like object within the solar system.

Jupiter
Jupiter is an immense celestial body situated nearly eight hundred million kilometers away from the Sun. This colossal giant is a staggering 315 times larger than the Earth. It boasts incredibly powerful winds, with speeds reaching up to six hundred kilometers per hour. Furthermore, Jupiter is home to mesmerizing polar auroras that rarely cease.
The radius and mass of this planet in our solar system is truly awe-inspiring, weighing in at 1.89 x 10^27 kg and having a diameter of nearly half a million kilometers (to put things into perspective, Earth’s diameter is a mere twelve thousand seven hundred kilometers).
Jupiter bears a striking resemblance to a self-contained system, with the planet acting as a radiant star around which numerous objects orbit. This impression is due to its multitude of satellites (67) and moons. It’s worth noting that if an individual weighs around forty-five kilograms on Earth, their weight on Jupiter would exceed a hundred centimeters.
Saturn
Saturn is positioned at a distance of nearly 1.5 billion kilometers away from the Sun. It is an awe-inspiring planet that boasts a remarkable ring system. The core of Saturn is surrounded by layers of gas.
This mesmerizing planet has a mass of approximately 5.66 x 10 26 kilograms. It completes one orbit around the Sun in nearly thirty Earth years. Despite the lengthy year, a day on Saturn lasts only eleven hours.
With a total of 53 satellites, Saturn is accompanied by a diverse group of moons. Additional discoveries have been made, uncovering nine potential satellites, but these findings have yet to be confirmed as belonging to Saturn.

Uranus: The Beautiful Giant Planet
Situated nearly three billion kilometers away, Uranus is a stunning giant planet. It falls under the category of an icy gas giant due to its atmospheric composition, which consists of methane, water, ammonia, and hydrocarbons. The abundance of methane in its atmosphere is responsible for its mesmerizing blue hue.
An Uranian year lasts for eighty-four Earth years, while a day on Uranus is relatively short, only lasting eighteen hours.
With a weight of 86.05 x 10^24 kg, Uranus is the fourth most massive planet in the solar system. It is an ice giant that boasts twenty-seven satellites and a small ring system.
Neptune
Located at a distance of 4.5 billion kilometers from the Sun, Neptune is an icy gas giant with its own set of satellites and a relatively weak ring system.
The planet has a mass of 1.02 x 10 26 kilograms and takes 165 years to complete one orbit around the Sun. A Neptunian day is a mere 16 hours in length.
Neptune’s atmosphere consists of water, methane, ammonia, and helium.
Neptune boasts a total of thirteen satellites, with one still awaiting official recognition as a moon. Among the planet’s ring system, scientists have identified six distinct formations. To date, only one man-made satellite, Voyager-2, has successfully reached this distant planet after being launched into space many years ago.
As gas giants, Neptune and its counterparts are known for their extreme cold, with temperatures plummeting to -300 degrees Celsius and beyond.

Pluto: A Former Ninth Planet
Pluto, once considered the ninth planet of the solar system, held its planetary status for a century before being reclassified as a dwarf planet in 2006. Despite its long history, much remains unknown about this celestial object. Scientists have yet to determine the length of a year on Pluto, as it was only discovered in 1930 and has completed less than a third of its orbital path.
Pluto has five known satellites and a relatively small diameter of only 2300 kilometers. However, it boasts a significant amount of water, estimated to be three times more than Earth’s water content. The planet’s surface is predominantly covered in ice, featuring visible ridges and dark patches.