What is the sidereal period?

• The sideric orbital period (derived from the Latin word “sidus” meaning star; genitive case “sideris”) refers to the duration in which a celestial satellite completes a full revolution around its main body in relation to the stars. The concept of the “sideric circulation period” is applicable to celestial bodies that orbit the Earth, such as the Moon (sideric month) and man-made satellites, as well as to planets, comets, and other objects that orbit around the Sun.

Related concepts

Main semi-axis – one of the primary geometric parameters of objects formed by utilizing a conic section.

Astronomical unit (Russian designation: a.e.; international: since 2012 – au; previously used designation ua) – historically established unit of distance measurement in astronomy. Initially, it was considered equal to the main semi-axis of the Earth’s orbit, which is considered the average distance from the Earth to the Sun: 126.

Aphelion or apogeolion (Greek. από “apo” – from, from (a prefix meaning negation and absence of something), Dr.-Greek ηλιος “helios” – the Sun) – the furthest point of a planet or other celestial body’s orbit from the Sun in the Solar System, as well as the distance from this point to the Sun.

Perihelion (from the Greek word “peri” meaning around or near, and the Greek word “helios” meaning the Sun) refers to the point in a planet or celestial body’s orbit around the Sun that is closest to the Sun.

Ecliptica (derived from the Latin term “ecliptica linea” and the Greek word “ekleipsis” meaning eclipse) is a large circle on the celestial sphere that represents the path of the Sun’s apparent annual motion. The ecliptic plane, therefore, corresponds to the plane of the Earth’s orbit around the Sun. A more precise definition of the ecliptic is the intersection of the celestial sphere with the orbital plane of the Earth-Moon system’s barycenter.

Literary References

When considering the compatibility of this theory with the observed movements of celestial bodies, it is important to note that it is unclear whether Eudoxus relied on actual observations to determine the magnitude of retrograde motions or if he simply recognized their existence without specific numerical data. In order to evaluate the theory, it is necessary to know the sideric period, synodic period, and the distance between the poles of the third and fourth spheres, referred to as the inclination by Schiaparelli. The specific value of this distance, as determined by Eudoxus for each planet, is not mentioned by either Aristotle or Simplicius, and the periods are only provided by Simplicius in approximate figures (p. 496).

Retrograde motion is the movement in a direction that is opposite to the direction of forward motion. This term can be used to describe the direction of rotation of one celestial body around another in an orbit or the rotation of a celestial body around its axis. It can also refer to other orbital parameters such as precession and nutation. In the context of planetary systems, retrograde motion generally refers to motion that is opposite to the rotation of the main body, which is the central object in the system.

An occultation is an astronomical phenomenon where one celestial body passes in front of another celestial body, obstructing a part of it. This phenomenon can be observed from a specific vantage point.

The Synodic Circumference Period (derived from the Greek word σύνοδος meaning conjunction) refers to the duration between two successive conjunctions of the Moon or any planet in the Solar System with the Sun as observed from Earth. It is important to note that these conjunctions of the planets with the Sun must occur in a specific linear sequence, particularly for the inner planets. For instance, this would involve consecutive upper conjunctions when a planet moves behind the Sun.

On the other hand, the Angular dimension (sometimes referred to as the angle of view) pertains to the angle formed by the straight lines that connect diametrically opposed extreme points of the object being measured or observed and the eye of the observer.

Opposition occurs when a celestial body in the solar system is positioned in such a way that the difference in its ecliptic longitude and the Sun’s is 180°. This means that the body is roughly aligned with the “Sun – Earth” line and can be observed from Earth in the opposite direction to the Sun. Opposition is only possible for planets and other celestial bodies that are further from the Sun than Earth.

In celestial mechanics, orbital resonance refers to a situation where the periods of revolution of two or more celestial bodies are related by small whole numbers. As a result, these bodies periodically come close to each other at specific points in their orbits. This regular fluctuation in the gravitational interaction between the bodies can help stabilize their orbits.

Epoch in astronomy (derived from the Greek word έποχή – “halt”) refers to a specific moment in time that is used to define astronomical coordinates or orbital elements. Astronomical coordinates can be converted from one epoch to another, while taking into account the effects of precession and proper motion.

The rotational period of a celestial object is the duration it takes for the object to complete one full revolution around its axis relative to the stars.

Rotational axis inclination refers to the angle by which the rotation axis of a celestial body deviates from being perpendicular to the plane of its orbit. In simpler terms, it is the angle between the equatorial plane of a celestial body and its orbit.

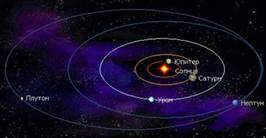
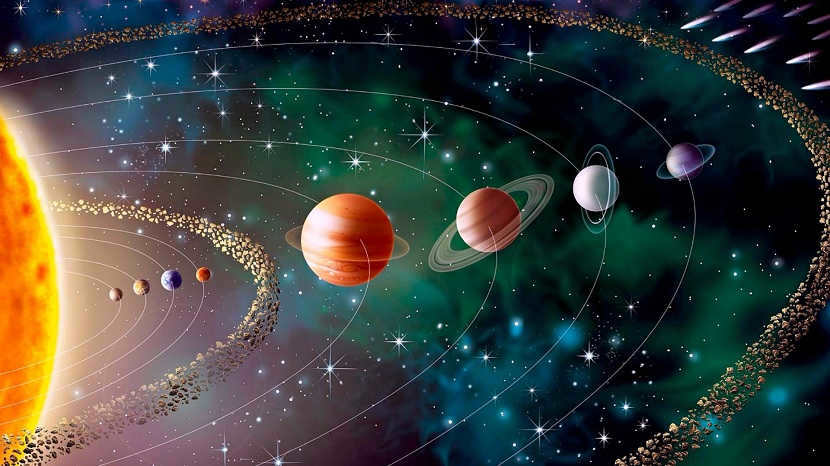
The giant planets are the four outer planets of the Solar System (Jupiter, Saturn, Uranus, and Neptune) situated beyond the asteroid belt. These planets, which share several physical characteristics, are also referred to as the outer planets.

Earth mass (designated M⊕ in astronomy, where ⊕ represents Earth) refers to the mass of the planet Earth and is utilized in astronomy as a unit of mass independent from the system. 1 M⊕ = (5.9722 ± 0.0006) × 1024 kg.

A transit, or astronomical transit, is an occurrence in astronomy when one celestial body passes in front of another celestial body, obscuring a portion of it, as observed from a specific vantage point.

Uranus is one of the planets in our Solar System, located as the seventh planet from the Sun. It is the third largest in terms of diameter and the fourth largest in terms of mass. The planet was officially discovered in 1781 by the English astronomer William Herschel. In honor of the Greek sky god Uranus, it was named after him.

The celestial sphere is a conceptual sphere with an arbitrary radius. It serves as a reference point for projecting celestial bodies and solving various astrometric problems. The observer’s eye is considered the center of the celestial sphere, whether they are on Earth’s surface or in other points of space. This rotation of the celestial sphere mirrors the daily movement of the stars and other celestial objects as seen from the perspective of a terrestrial observer.

Observation arc refers to the time period between the initial and most recent observations that track the path of an object. The duration of the observation arc is typically measured in days or years. This term is commonly used in the context of identifying and monitoring the movements of asteroids and comets.

Lagrange points, also known as libration points (derived from the Latin word “librātiō” which means swaying), are specific points within a system consisting of two massive bodies. At these points, a third body with negligible mass can stay stationary in relation to the two larger bodies, solely influenced by the gravitational forces exerted by them.

The solar system encompasses a planetary system that revolves around the central star, which is the Sun. It includes all natural celestial objects that orbit around the Sun. The solar system took shape approximately 4.57 billion years ago through the gravitational collapse of a gas and dust cloud.

An elliptical orbit is a type of Keplerian orbit in astrodynamics and celestial mechanics. It is characterized by having an eccentricity less than 1. A circular orbit, on the other hand, is a specific case of an elliptical orbit with an eccentricity of 0. In a stricter definition of an elliptical orbit, circular orbits are not considered, so elliptical orbits have eccentricities that are greater than zero but less than one. In a broader sense, an elliptical orbit can be defined as a Keplerian orbit with negative energy, which also encompasses radial orbits.

Synchronous rotation (also known as tidal capture) occurs when the time it takes for a satellite to rotate around its axis matches the time it takes for it to orbit around the central body. As a result, the satellite always presents the same side to the central body, since it completes one rotation on its axis in the same amount of time it takes to complete one orbit around its partner. Tidal capture happens during the mutual motion of the two bodies and is a common feature observed in many of the large natural satellites orbiting planets in the solar system.

Eryda, also known as 136199 Eris in the CMP catalog, holds the distinction of being the second largest dwarf planet in our Solar System, coming in just behind Pluto. It is not only the most massive but also the farthest planet from the Sun. In the past, it went by the name Xena. Eryda falls into the category of trans-Neptunian objects known as plutoids. Prior to the XXVI Assembly of the International Astronomical Union, Erida was once considered the tenth planet. However, on August 24, 2006, the International Astronomical Union redefined what qualifies as a classical planet, and both Erida and Pluto no longer meet the criteria.

Mercury, the closest planet to the Sun in our Solar System, is also the smallest of the terrestrial planets. It draws its name from the fast-moving Roman god of commerce, Mercury, as it swiftly courses through the celestial sphere at a quicker pace than any other planet.

A Julian year (symbol: a) is a unit of time measurement. It is equivalent to 365.25 Julian days, with each Julian day consisting of 86,400 SI seconds. This totals exactly 31,557,600 seconds. The Julian year represents the average length of a year in the Julian calendar, which was used in Europe during ancient times and the Middle Ages.

In astronomy, Julian years are utilized to express the orbital periods of objects in the solar system, such as asteroids and comets. They are also employed in geochronology for measuring long spans of time, as well as in nuclear science.

Orbital elements, also known as celestial body orbital elements, encompass a collection of parameters that define the size and shape of a celestial body’s orbit. These elements also specify the position of the orbit in space and the location of the celestial body within the orbit.

Declination (δ) is a fundamental concept in the field of astronomy. It is one of the two coordinates used in the equatorial coordinate system, with the other being right ascension. Declination represents the angular distance on the celestial sphere from the plane of the celestial equator to a celestial object, such as a star or a planet. This distance is usually measured in degrees, minutes, and seconds of arc. It’s important to note that declination can be positive when measured north of the celestial equator, and negative when measured south of it.

The brightness of an object is measured using a dimensionless numerical characteristic called stellar magnitude, denoted by the letter m (from Latin magnitudo “magnitude, size”). This concept is commonly used to describe the brightness of celestial objects. Stellar magnitude depends on the energy flux emitted by the object (the energy of all photons per second) per unit area. Therefore, the apparent stellar magnitude is influenced by both the object’s physical characteristics (such as luminosity) and its distance from us. A smaller stellar magnitude value indicates a lower brightness.

Super-Earth refers to a class of planets that have a mass greater than Earth’s but significantly less than that of gas giants. The term “super-Earth” specifically describes the mass of a planet and does not take into account its proximity to its star or any other criteria.

Absolute stellar magnitude is a physical quantity that describes the brightness of an astronomical object. Various definitions of absolute magnitude are used for different categories of objects.

Extraterrestrial skies refer to the view of space from the surface of a celestial body other than Earth. This perspective can differ from what is observed from Earth’s surface for several reasons. The primary factor is the atmosphere of the celestial body, or the lack thereof. The color of the sky is influenced by the density and chemical composition of the atmosphere. Clouds may or may not be present and their color can vary. Other factors include the presence of astronomical objects visible from the surface, such as stars, satellites, planets, and rings.

Gas giants are celestial bodies primarily composed of hydrogen, helium, ammonia, methane, and various other gases. These types of planets have a relatively low density, a short diurnal rotation period, and as a result, experience significant compression at their poles. The visible surfaces of gas giants reflect or scatter the rays of the sun.

Right ascension (α, R. A. – derived from the English term right ascension) refers to the measurement of the arc length along the celestial equator from the point of the vernal equinox to the circle of declination of a celestial object. It is one of the coordinates used in the second equatorial system (there is also a first equatorial system that utilizes the hour angle). The second coordinate is known as declination.

Jupiter, the largest planet in our Solar System, is also the fifth farthest from the Sun. It is classified as a gas giant, along with Saturn, Uranus, and Neptune.

A quasi-sputnik is an object that is similar to, or something like, a planet and is in 1:1 orbital resonance with it. This allows the quasi-sputnik to remain in close proximity to the planet for multiple orbital periods.

The Oort cloud is a hypothetical, spherical region within the solar system that is believed to be the source of long-period comets. While the existence of the Oort cloud has not been directly confirmed, there are numerous indirect pieces of evidence that suggest its presence.

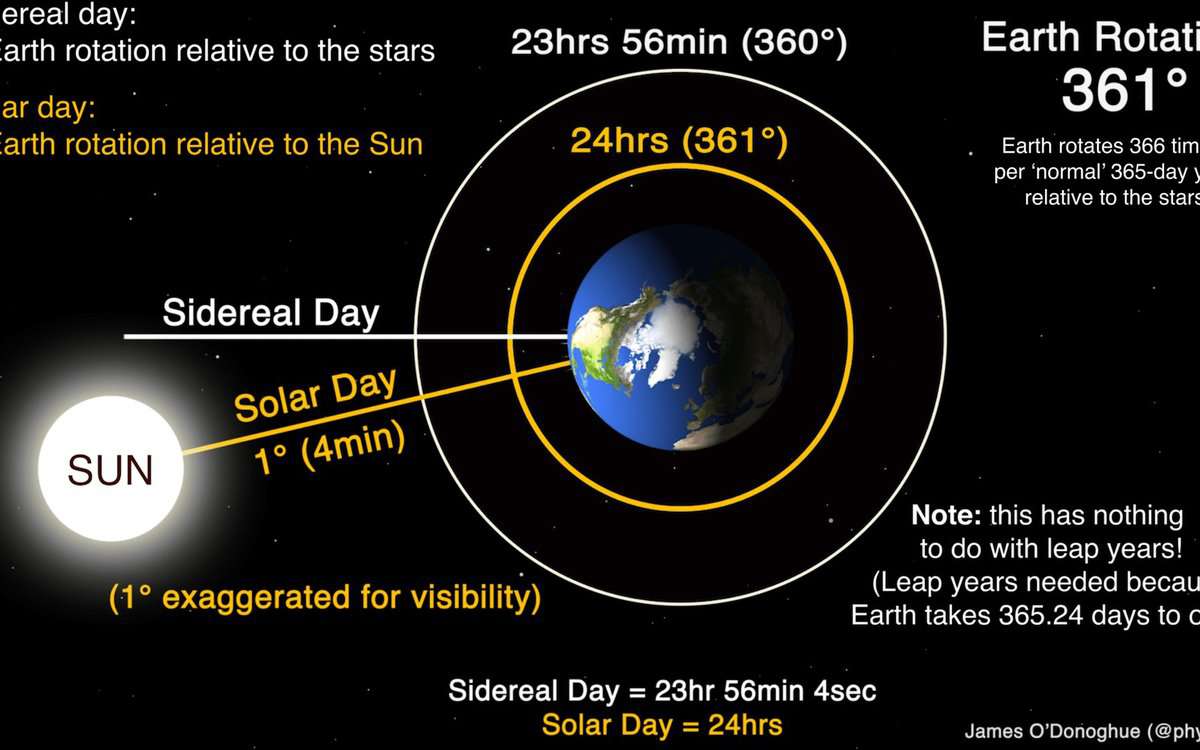
Stellar days refer to the period of rotation of a celestial body around its own axis in an inertial frame of reference. This frame of reference is typically associated with distant stars. For Earth, a stellar day is the time it takes for the planet to complete one full revolution around its axis in relation to the distant stars.

Planet (derived from the Greek word πλανήτης, an alternate form of the Greek word πλάνης – “wanderer”) is a celestial object that orbits a star or its remnants. It is large enough to be rounded by its own gravity, but not massive enough to initiate a thermonuclear reaction. Additionally, a planet has the ability to clear its orbit of planetesimals.

Kirkwood gaps refer to specific regions within the asteroid belt that are formed due to the resonant influence of Jupiter. These areas are characterized by a lack of asteroids.

An Astronomical Object or Celestial Body is a natural physical entity, organization, or arrangement that is recognized by modern science as being located within the visible universe. The phrase “astronomical object” is frequently used interchangeably with the term “body”. Usually, a “celestial body” refers to a separate, individual structure that is held together by gravitational forces (and sometimes electromagnetic forces) such as asteroids, satellites, planets, and stars. “Astronomical objects” are structures that are bound together by gravitational forces.

The celestial sphere has a point known as the Pole of the World, where the stars appear to move in a circular motion due to the Earth’s rotation. The North Pole of the World aligns with the Earth’s geographical north, while the South Pole of the World aligns with the Earth’s geographical south. In the constellation of the Little Bear, the North Pole of the World can be found, specifically with the star Polaris. The South Pole of the World can be found in the constellation Octanthus. Over time, the Earth’s axis undergoes precession, causing the poles of the World to shift at a rate of approximately 20 arcseconds per year.

The celestial equator is a vast circle on the celestial sphere that is perpendicular to the Earth’s axis and aligns with the Earth’s equator. This circle divides the celestial sphere into two hemispheres: the northern hemisphere, centered around the north pole of the Earth, and the southern hemisphere, centered around the south pole of the Earth. The constellations that the celestial equator passes through are known as equatorial constellations.

In 2006, the XXVI Assembly of the International Astronomical Union defined a dwarf planet as a celestial body that.

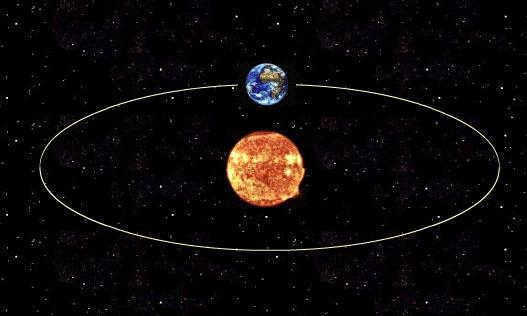
The path of the Earth’s movement around the Sun is known as the Earth’s orbit, and it spans an average distance of approximately 149.6 million kilometers (152.1 million km at its farthest point, known as aphelion, and 147.09 million km at its closest point, known as perihelion).

In the time of Isaac Newton, the study of the stars and their movement was referred to as “celestial mechanics,” and it followed the classical laws governing the motion of objects. One interesting aspect of this motion is the different periods of orbital movement for celestial bodies. This article will explore the sidereal and synodic orbital periods of stars, planets, and their natural satellites.

The notion of synodic and sideric time intervals

We are all familiar with the fact that planets orbit their stars in elliptical paths. Likewise, stars orbit either each other or the center of the galaxy. This means that all massive objects in space, including comets and asteroids, have specific paths they follow.

One important characteristic of any object in space is the amount of time it takes to complete one full revolution along its path. This is commonly known as its period. In astronomy, there are two periods that are often used to study the Solar System: the synodic period and the sideric period.

The sideric period refers to the duration it takes for an object to complete a full revolution in its orbit around its star, using another distant star as a point of reference. It is also known as the true period, as it represents the actual time it takes for the object to complete its orbital rotation around its star, according to an observer at rest.

The synodic period, on the other hand, represents the time it takes for the object to reappear at the same position in the sky when observed from any planet. For example, if we consider the Moon, the Earth, and the Sun, the synodic period of the Moon would be the time it takes for the Moon to return to its current position in the sky. This period is also referred to as the apparent period, as it differs from the actual orbital period.

As previously mentioned, the sideric period represents the true duration of orbit, while the synodic period represents the apparent duration. However, what sets these concepts apart?

The distinction lies in the number of objects used as reference points for measuring time. The concept of the “sideric period” considers only one reference object, such as Mars orbiting around the Sun, thus measuring the movement relative to a single star. On the other hand, the synodic period is a characteristic that takes into account the relative positions of two or more objects, such as two identical positions of Jupiter in relation to an observer on Earth. In this case, the position of Jupiter must be considered not only relative to the Sun, but also in relation to Earth, which also orbits around the Sun.

Equation for computing the sideric period

To calculate the actual orbital period of a planet around its star or a natural satellite around its planet, the application of Kepler’s third law is necessary. This law establishes the relationship between the actual orbital period of an object and the semi-major axis of its orbit. In general, the shape of any cosmic body’s orbit is an ellipse.

The formula for determining the sideric period is as follows: T = 2*pi*√(a3/(G*M)), where pi = 3.14 represents the value of pi, a is the semi-major axis of the ellipse, G = 6.674*10-11 m3/(kg*s2) is the universal gravitational constant, and M is the mass of the object around which the orbit is performed.

Therefore, by having knowledge of the orbital parameters of any entity, along with the star’s mass, one can easily determine the actual orbital period of said entity.

Determining the Synodic Time Period

How is it calculated? The synodic period of a planet or its natural satellite can be calculated by knowing the actual orbital period of the entity around the subject in question and the actual orbital period of the subject around its star.

The formula used for such calculations is: 1/P = 1/T ± 1/S, where P represents the actual revolution period of the entity in question, T is the actual revolution period of the entity around the subject, and S is the unknown synodic time period.

The symbol “±” in the equation should be utilized in the following manner: if T is greater than S, then the equation is applied with the symbol “+”, if T is less than S, then the equation is applied with the symbol “-“.

Sideric vs. Synodic

The comparison between sideric and synodic time is an interesting topic in astronomy. Sideric time refers to the time it takes for a celestial object to complete one full orbit around another object, usually a star. On the other hand, synodic time refers to the time it takes for a celestial object to return to the same relative position as seen from Earth.

In simpler terms, sideric time is the time it takes for a planet to complete a full orbit around the Sun, while synodic time is the time it takes for a planet to complete a full cycle of phases as seen from Earth.

The difference between sideric and synodic time can be seen in the example of the Moon. The Moon’s sideric period is about 27.3 days, which is the time it takes for the Moon to complete one orbit around the Earth. However, the synodic period of the Moon is about 29.5 days, which is the time it takes for the Moon to return to the same phase as seen from Earth.

This difference occurs because while the Moon is orbiting the Earth, the Earth is also moving around the Sun. So, in order for the Moon to return to the same phase as seen from Earth, it has to complete a few extra degrees of its orbit.

In conclusion, sideric and synodic time are two different ways of measuring the time it takes for a celestial object to complete a full cycle. Sideric time is based on the object’s orbit around another object, while synodic time is based on the object’s position as seen from Earth.

Sideric and Synodic are two distinct terms used in the field of astronomy, and they have significant distinctions between them. Both terms relate to the orbital motion of celestial bodies. Sidereal refers to the amount of time it takes for a star to complete one full revolution. Conversely, Synodic refers to the amount of time it takes for a solar body to complete one full revolution. This is the primary difference between Sidereal and Synodic. To further illustrate, a sidereal day is the duration it takes for a star to return to its exact position. On the other hand, a synodic day is the duration it takes for the Sun to pass the meridian of an observer. The origins of these terms differ as well. “Sidus” is a Latin word meaning star, which serves as the basis for the term “sideric.” On the contrary, the term synodic is derived from the Greek word “synodos,” meaning “meeting of two things.”

What does sideric mean?

In astronomy, the term sideric refers to the position of objects in relation to the stars. The sidereal period is the time it takes for an object to complete one revolution around the Earth in relation to the stars. This is equivalent to a sidereal day, which is the time it takes for the Earth to rotate 360 degrees and return to its original position in relation to the stars. It is worth mentioning that a sidereal month is relatively short, lasting approximately 27 days, 7 hours, and 43 minutes.

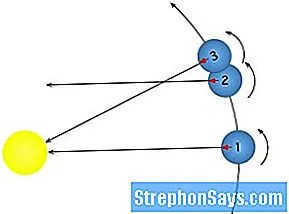
1-2 = one sideral day
1 through 3 = one synodic day

What does synodic mean?

The synodic period refers to the position of objects relative to the Sun. When it comes to a synodic day, it means the Earth rotates once a day in relation to the Sun. One might think that this would mean the Earth only rotates 360 degrees. However, that is not the case. Due to the Earth’s continuous movement around the Sun, it must rotate slightly more than 360 degrees for the Sun to be on the observer’s meridian. A synodic day is also known as a solar day. It is noteworthy that the synodic month is longer. In other words, the synodic month is slightly longer than the sideric month. On the flip side, the synodic month lasts 29 days, 12 hours, and 44 minutes. The period of time from one full moon to another full moon is referred to as the synodic cycle.

What is the distinction between sideric and synodic?

– The time it takes for the stars to complete a period is known as the Sidereal. On the contrary, the Synodic is the time required for the solar body to complete a period. This is the primary distinction between siderial and synodic.

– A sidereal day refers to the duration it takes for a star to return to its exact position. A synodic day, on the other hand, refers to the time it takes for the Sun to pass the observer’s meridian. A synodic day is also referred to as a solar day.

– The synodic period refers to the position of objects in relation to the Sun. Conversely, the stellar period refers to the position of objects in relation to the stars. This is another significant difference between the two terms.

– It is worth noting that there are two different types of months, known as the sidereal month and the synodic month, which have different durations. The synodic month is said to be slightly longer than the sidereal month.

– More precisely, the sidereal month is said to last 27 days, 7 hours, and 43 minutes. On the other hand, the synodic month has a duration of 29 days, 12 hours, and 44 minutes.

– In order to complete one sidereal day, the Earth needs to rotate 360 degrees. However, to complete one synodic day, the Earth needs to rotate slightly more than 360 degrees.

This is the distinction between siderial and synodic. As you can observe, the Siderial is connected to the stars, while the Synodic is linked to the Sun.

Images courtesy of:

Paragraph 11, “Planetary Configurations. The Synodic Period.”

Strategy

1. Positions of planets in opposition and conjunction

2. Higher and lower conjunction

3. Synodic and sidereal periods of planetary orbits

Objective of education:

Educational goal: Expanding the conceptual foundation by incorporating knowledge about the opposition and conjunction of planets, as well as the synodic and sideric (sidereal) periods of planetary orbits. Systematizing concepts about celestial phenomena, such as the visible motion and configurations of planets observed as a result of the mutual movement and positioning of celestial bodies relative to the Earth observer. Providing a detailed examination of the causes and characteristics of the cosmic phenomenon of planetary orbits around the Sun and its consequences – celestial phenomena: the visible motion of inner and outer planets in the sky.

Activity objective: Developing the students’ ability to approach a new way of action: teaching them to determine the conditions of planet visibility.

Expected Results

1. Provide an assessment of the reliability of methods used to gather information about the visibility of planets;

2. Engage in discussions about the findings and conclusions obtained from analysis;

3. Demonstrate interest in conducting independent observations of planets.

1. Apply physical laws and principles to explain the factors influencing planetary visibility;

2. Formulate logically sound conclusions based on the patterns identified through analysis.

1. Identify the type of configuration and perform basic calculations to determine the periods of revolution; utilize astronomical calendars, reference materials, and a dynamic star map to identify the conditions for the occurrence and progression of specific celestial phenomena.

2. The objective is to address issues related to calculating the position and visibility conditions of planets by considering formulas that express the relationship between their sidereal and synodic periods of circulation and rotation.

1. Motivational Stage (Self-Determination) for Learning Activity

O celestial bodies! O congregation of sacred bees!
I have conducted surveys, measurements, and calculations,
I have assigned names and created maps.
Yet the awe-inspiring nature of the stars remains untouched by knowledge.
M. Voloshin

1 The zenith refers to the point on the celestial sphere directly above an observer’s head.

2 Venus is a planet that belongs to the earth group of the solar system.

3 Culmination is the phenomenon of the passage of the celestial meridian.

4 Calendar is the system used to count time.

2 Document and address individual challenges encountered during the trial activity.

Determine the causes of celestial phenomena by marking the correct answer choice number for each question option, for example, A1; B2; C3, etc.

A. The movement of the stars in the sky becomes visible
B. The seasons change
C. Day and night alternate
D. The moon goes through different phases
E. The Sun moves across the sky during the day
F. Solar eclipses occur
G. The Sun’s altitude above the horizon changes over the course of a year
H. Lunar eclipses happen

I. The synodic period of planetary orbits

J. The sidereal period of planetary rotation

K. The upper conjunction of the planets

1) The Earth rotates on its axis;
2) The Moon orbits around the Earth;
3) The Earth orbits around the Sun.
Correct answers:
A1; B3; C1; D2; E1; F1; G2; H3; I2

3. The stage of identifying the place and cause of difficulties

4. Creating a project to find a solution to the situation.

What information do we need to gather for this purpose?

Write it down on the board (using the Brainstorming method).

5. Implementing the developed project.

Engage in the following cases:

1. Working on the case “Composition of the Solar System”.
2. Working on the case “Loop motion”.
3. Working on the case “Configuration of planets”.
4. Working on the case “Periods of planetary orbits”.

1. Composition of the solar system:

1. Currently, there are a total of 8 large planets in our solar system that possess satellites and rings. These planets include Mercury, Venus, Earth (accompanied by the Moon), Mars (with its moons Phobos and Deimos), Jupiter (which has a ring and a minimum of 63 satellites), Saturn (known for its powerful ring system and at least 60 satellites), Uranus (discovered in 1781, featuring a ring and at least 27 satellites), and Neptune (discovered in 1846, with a ring and at least 13 satellites).

2. Dwarf planets are a separate category of celestial bodies. Examples include Pluto (discovered in 1930 and initially considered a planet until August 24, 2006), Ceres (the first asteroid ever discovered in 1801), and objects located within the Kuiper Belt, such as Xena (officially named 136199 Eris, also known as object 2003UB313) and Sedna (object 90377). These objects exist beyond the orbit of Pluto and were discovered in 2003.

3. Asteroids, including the first Ceres discovered in 1801 (which was reclassified as a dwarf planet on 24.08.2006), are primarily found in four belts: the Main Belt, located between the orbits of Mars and Jupiter; the Kuiper Belt, situated beyond the orbit of Neptune; and the Trojans, which occupy the orbits of Jupiter and Neptune. These minor planets are typically less than 800 kilometers in size, and there are currently almost 400,000 known asteroids.

4. Comets are small bodies, with diameters of up to 100 km, composed of dust and ice. They follow highly elongated orbits, and the Oort Cloud, which serves as a reservoir for comets, is located on the outermost fringes of the solar system.

5. Meteoric bodies encompass a wide range of sizes, from grains of sand to rocks several meters in diameter. They are formed from comets and fragmented asteroids. Smaller meteoric bodies burn up upon entering Earth’s atmosphere, while larger ones that survive the descent and reach the Earth’s surface are known as meteorites.

6. Interplanetary dust originates from the crushing of comets and asteroids. Smaller particles are pushed towards the outer edges of the solar system due to solar pressure, while larger particles are attracted by the gravitational pull of the planets and the Sun.

7. The interplanetary gas found in the solar system is extremely thin. It consists of the “solar wind,” which is a stream of plasma (ionized gas from the Sun) that propagates through it.

8. Electromagnetic radiation and gravitational fields permeate the solar system. It is filled with magnetic fields generated by the Sun and the planets, as well as gravitational fields and electromagnetic waves of various wavelengths emitted by the planets and the Sun.

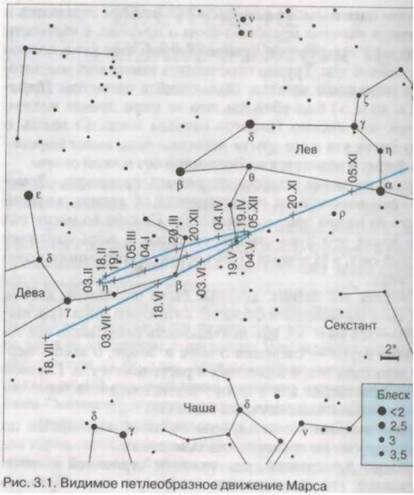
2. The planets orbit in a looping motion

3. Planetary Configuration.

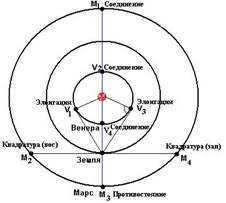
Configuration refers to the specific arrangement of the planets in relation to the Sun and the Earth.
A conjunction occurs when a planet is in alignment with the Sun and the Earth, either above or below the straight line connecting them. An elongation occurs when a planet is at its farthest angular distance from the Sun, either to the west or the east. This is the best time to observe planets like Mercury (at 28°) and Venus (at 48°).
During a lower conjunction, both Venus and Mercury occasionally cross the Sun’s disk.
Mercury does this 13 times every 100 years, typically in May and November. The most recent occurrences were on May 7, 2003 and November 8, 2006, and the next ones will be on May 9, 2016 and November 11, 2019.
Venus also crosses the Sun’s disk, but at a different frequency of 8 times every 105.5 years, or 8 times every 121.5 years. The last crossing was on June 8, 2004, and the next one will be on June 6, 2012.

Upper – quadrature (west and east – quarter circle) and conjunction (opposition – when the planet is behind the Earth from the Sun – the optimal time to observe the outer planets, as they are fully illuminated by the Sun).

4. Periods of planetary orbits.
During the development of the heliocentric model of the universe, N. Copernicus derived the formulas (equations of the synodic period) for calculating the periods of planetary orbits and calculated them for the first time.
Sidereal (T – stellar) – the time interval during which a planet completes a full revolution around the Sun in its orbit relative to the stars.
Synodic (S) – the time interval between two consecutive identical configurations of a planet.

Planets that are closer to Earth orbit at a faster pace, while those farther away orbit at a slower pace.
If a planet completes a full revolution in a period of T, then in a day it will orbit the Earth by 360 o /T and the Earth by 360 o /Tз.
Therefore, for a planet closer to Earth, the difference in average distances is the observed daily displacement 360 o /S=360 o /T – 360 o /Tз or 1/S=1/T – 1/Tз (form.12), while for a planet farther away, it is 1/S=1/Tз – 1/T (form.13).

internal external

The Earth’s atmosphere causes sunlight to scatter on random microscopic variations in air density and rarefactions that have sizes ranging from 10^-3 to 10^-9 meters. This scattering of light follows Rayleigh’s law, where the intensity of scattering is inversely proportional to the fourth power of the wavelength. Shorter wavelengths such as violet, blue, and cyan rays are scattered more strongly, while longer wavelengths like orange and red rays are scattered less. This is why the sky appears blue during the day. Even at night, the Earth is never completely dark because the light from stars and the residual scattering of the Sun’s light in the atmosphere creates a faint illumination of 0.0003 lux.
The duration of daylight, or the time from sunrise to sunset, is always shorter than the length of the day. This is because the scattering of the Sun’s rays in the atmosphere gives rise to twilight, a gradual transition between day and night. Twilight occurs because the upper atmosphere is still illuminated by the Sun even when it is below the horizon line. The duration of twilight depends on the position of the Sun on the ecliptic and the geographical latitude of a location.
Therefore, a distinction can be made between the length of the day and the duration of twilight.

6. Self-study phase with validation against a benchmark

Celestial events that occur as a consequence of these cosmic phenomena

1) The phenomenon of atmospheric refraction leads to:
– the distortion of the celestial coordinates of stars;
– the need to make corrections to the equatorial coordinates of celestial objects due to refraction;
– the distortion of the shape and angular sizes of stars at sunrise and sunset due to their elevation;
– the twinkling of stars;
– the occurrence of the “green ray” phenomenon.
2) Light scattering in the Earth’s atmosphere results in:
– the blue color of the daytime sky;
– the blue and lilac hues of the evening and morning sky;
– the phenomenon of twilight;
– the duration of daylight hours always being longer than the time interval from sunrise to sunset;
– the occurrence of white nights; polar day and polar night at high latitudes;
– the glow of the night sky;
– the occurrence of dawn; the red color of dawn;
– the reddening of the Sun and Moon disks during sunrise and sunset.

7. Initial consolidation stage involving pronunciation of external speech.

Engage in problem-solving activities..

1. The luminary is located in the west side of the sky when its azimuth is 45° and its altitude is 60°.
2. The star with coordinates α=4 h 14 m, δ=16°28′ is located in the constellation Taurus, specifically the star Aldebaran.
3. The zenith distance of the Sun is 90° during sunrise and sunset.
4. In 1918, due to the reform, the calendar in the Russian Federation contained 352 days (365 days minus 13 days).
5. A planet is considered upper when it is visible at a distance of 120° from the Sun.
6. During the Mars opposition on March 20, 1997, Mars was in the constellation Pisces, specifically at the point γ.
7. If an astronaut observed the starry sky from Mars, would the constellation configuration visible from Earth remain unchanged? [yes].

5. What are the conditions for Earth to be visible from the Moon’s surface? How about from the orbit of Venus’ satellite? What about from the surface of Mars? (Take into account the Sun’s position and its interference with visibility).

6. If there are 780 days between two oppositions, what is the length of a year on Mars? (1/S = 1/Tз – 1/Т hence T = (Tз . S) / (S – Tз) = (365.25 . 780) / (780 – 365.25) = 686.9 days)

8. When observing Mercury, it is most convenient to do so near its elongations. Why is that? And how often do these elongations occur if the year on Mercury is 88 days? (They are less interfered with by the light of the Sun, 1/S = 1/T – 1/Tз hence S = (88 . 365.25) / (365.25 – 88) = 115.9 days)

9. The opposition of Jupiter was observed on April 30, 1994, at 13.9 hours. When will the next opposition be? And will it be visible?

Solution: By utilizing the formula 13, we can calculate that S = 1.092 years = 1.092 * 365.25 = 1 year + 34 days. By adding this duration to the given date, we can determine that the opposition occurred on June 2, 1995. As per PKZN, we can observe the constellation of Serpens between 16 and 17 hours, although it is not visible during the daytime.

1) What is the definition and classification of a configuration?

2) Can you explain the difference between sideric and synodic periods?

3) What are the constituents of the solar system?

4) Why aren’t the positions of planets indicated on star charts?

5) Which constellations should we search for planets in the sky?

6) Identify the planets that can be observed against the backdrop of the Sun’s disk.

7) Submit a test paper, crossword puzzle, report, and questionnaire (detailing their completion and the questions asked) on the first chapter of “Introduction to Astronomy”.

Assignment: §11; create a map of intelligence.
* Tasks from the collection of Olympiad tasks by V.G. Surdin:
4.10. On Earth, the length of the solar day is longer than the length of the sidereal day, but on Venus, it is the opposite. Why? (To solve this problem, it is necessary to remember that the Earth rotates on its axis in the opposite direction to its rotation around the Sun. Venus is the only planet in the solar system that rotates in the same direction as its rotation around the Sun. On Venus, the Sun sets below the horizon before the stars with which it rose at the same time).
4.13. It is said that Venus can be seen either in the morning or in the evening. Is it possible to observe Venus during both morning and evening of the same day? (The answer is “yes”. The phenomenon of “double visibility” of Venus is observed when there is a significant difference between the declinations of the Sun and Venus. In this case, in the middle and northern latitudes, Venus rises slightly earlier than the Sun and sets slightly later than the Sun).

9. Reflection stage of the lesson’s learning activity

Synquain “Planet Configurations”

In the era of Isaac Newton, the field of studying celestial bodies was often referred to as “celestial mechanics”. This discipline follows the classical principles of motion governing bodies. Among the notable attributes of this motion are the distinct periods during which space objects complete their orbits. This article will delve into the sideric and synodic periods of orbital motion concerning stars, planets, and their respective moons.

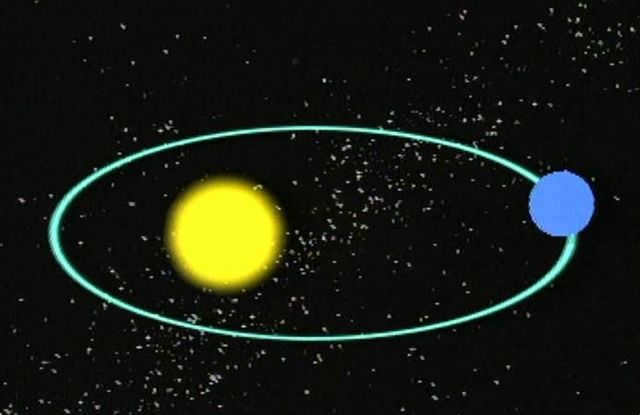
It is widely known that planets have elliptical orbits around their stars. Similarly, stars can orbit around each other or the center of the Galaxy. This means that all objects in space, including comets and asteroids, have specific trajectories.

One key aspect of any space object is the amount of time it takes to complete one full revolution along its trajectory. This is known as a period. In the field of astronomy, particularly when studying the Solar System, two types of periods are commonly used: synodic and sideric periods.

The sideric time period refers to the duration it takes for an object to complete a full revolution in its orbit around its star, using another distant star as a reference point. This period is also known as the true period, as it represents the actual time it takes for the object to rotate around its star, as observed by a stationary observer.

The synodic period, on the other hand, represents the time it takes for the object to reappear at the same position in the sky when viewed from any planet. For instance, if we consider the Moon, the Earth, and the Sun, and want to determine how long it will take for the Moon to return to its current position in the sky, the answer would be the Moon’s synodic period. This period is also referred to as the apparent period, as it differs from the true orbital period.

The primary distinction between sideric and synodic periods

As previously stated, the sideric period represents the actual time it takes for an object to complete one orbit, while the synodic period refers to the perceived time it takes for the object to return to the same position in relation to another celestial body. So, what sets these concepts apart?

Formula for calculating the sidereal period

In order to calculate the actual time it takes for a planet to orbit its star, or for a natural satellite to orbit its planet, it is necessary to apply Kepler’s third law. This law describes the relationship between the orbital period of an object and the length of its major axis. Generally, the orbit of any celestial body takes the shape of an ellipse.

The formula for calculating the sideric period is: T = 2*pi*√(a3/(G*M)), where pi = 3.14 represents the mathematical constant pi, a is the semi-major axis of the ellipse, G = 6.674*10-11 m3/(kg*s2) represents the universal gravitational constant, and M is the mass of the object around which the orbit is performed.

Therefore, by having the orbital parameters of any entity and the star’s mass, it becomes simple to determine the actual orbital period of said entity.

Calculation of the synodic time period

How to perform the calculation? The synodic period of a planet or its natural satellite can be determined by knowing the actual orbital period of the said entity around the object in question and the actual orbital period of this object around its star.

The formula used for this calculation is as follows: 1/P = 1/T ± 1/S, where P represents the actual revolution period of the entity under consideration, T represents the actual revolution period of the entity around its star, and S represents the unknown synodic time period.

The symbol “±” in the equation needs to be applied as follows: if T is greater than S, then the equation is used with a plus sign “+”, if T is less than S, then the equation should be used with a minus sign “-“.

Applying the equation to the Moon as an example